真实与幻想的夜想曲
sidekick257
·
·
题解
土归土,灰归灰,尘归尘,幻归幻。然后,梦归梦。
算法一
容易发现本题的操作是线性基状物,将矩阵拍扁成一维数组后(从左到右从上到下标号),丢入线性基暴力求解,答案是 2^{线性基大小}。
复杂度 O(\frac{(nm)^3+nm(x+y)}{w})。
算法二
我们称一个格子可控当他在线性基中为 1。
我们称线性基矩阵为对应的格子在线性基中是否可控。
考虑 x=a=b,y=c=d 时。
令 x<y,z=\gcd(x,y)。
棋盘足够大的情况
我们不妨先假设 n 和 m 对于 x 和 y 足够大。
我们先将所有 x\times x 的矩阵填入,我们会得到线性基矩阵中的一个在左上角的 (n-x+1)\times(m-x+1) 矩形。
注意力比较集中的同学可以发现两种特殊矩阵的构造(这是等下要用到的神秘妙妙工具),分别是:
- 在上方 x 行中只有右侧的 z 行有 1 的矩阵,下 y-x 行随意。
- 只在 z\times(x+y-z) 内有 1 的矩阵。
矩阵 1
矩阵一是用 x\times x 的矩阵和 y\times y 的矩阵模拟辗转相减得到的。
模拟方式:一开始是 y\times y 的矩阵,接下来在左上角不断相邻的异或 x\times x 的矩阵,直到再异或会超出 y\times y 的范围,此时的上方 x 行只有右侧的 y\bmod x 列有 1。
接下来我们对于一个 x\times x 的矩阵,用刚才得到的 y\bmod x 的矩阵来进行这个操作,不难发现右侧会变成只有 x\bmod (y\bmod x) 有 1。
不难发现事实上就是辗转相减,所以最后会变成只有右侧 z 列有 1。
矩阵 2
不难发现实际上可以做到使矩阵只有下 y\bmod x 行有 1。
我们用在辗转相除中得到的最后一个矩阵把倒数第二个矩阵的上方消完。
断言:这个矩阵只看其中一行(因为对于下面的 y\bmod x 行不难发现是全部相同的,所以我们考虑其中一行的性质)非零且可以被 1\times x 的矩阵减为全零。
如果是这样,那么就可以像矩阵 1 的辗转相减一样来使这个矩阵的高变为 z 了。
接下来我们来证明这个事实。
只考虑 z=1 的情况,若 z\ne1 视作将 x 和 y 同时除 z。
我们发现,只看一行时一定是若干个 1\times y 构造出的,我们断言:其一定是在开头连续的 x 个 1\times y。
事实上是相邻两个间隔为 z-1。
我们设辗转相除的数组一共有 k 项,为 a_1\dots a_k 。
我们设 x 代表在位置 x(从左到右)放一个 1\times y。
那么观察一下我们在干的事情。
$1+a_1$。
$1+a_2$。
$1+a_3$,$1+a_1+a_3$。
$1+a_4$,$1+a_1+a_4$,$1+a_2+a_4$。
这个是每相邻两项的商为 $1$ 时的结果,商不为 $1$ 时是类似的。
容易发现,这个显然是不会重复的,因为 $a_i\ge a_{i+1}+a_{i+2}$,丢到数轴上不难发现某个数加一个新数一定小于其下一个数。
数量显然恰好是对的,且大的一项为 $x$,故证明完毕。
#### 然后呢?
我们考虑在线性基矩阵中为 $1$ 的格子的形状,我们会发现左上角有一个矩形可以填满(对应下图红色部分),然后紧接着右边有一个矩形使用我们得到的矩阵一来填满(对应下图蓝色部分),然后接着下方有一个矩形可以用我们得到的矩阵二来填满(对应下图黄色部分),棕色的部分的厚度是 $z-1$。
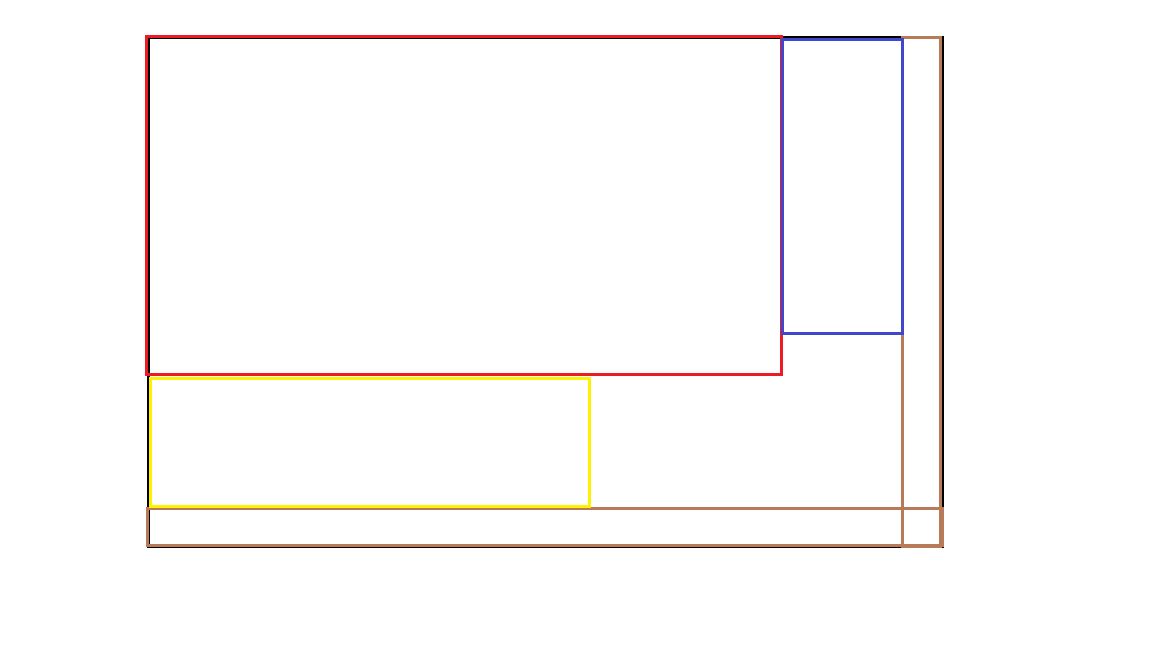
我们可以简单的计算答案 $ans=n\times m-((z-1)\times(n+m)-(z-1)^2)-2(x-z)(y-z)$。
事实上,当 $n,m\ge x+y-z-1$ 时即可取到此值。(证明见后几段)。
### 棋盘不够大的情况
接下来我们考察棋盘不够大的情况。
#### 蓝色部分
我们称二元组 $(a,b)$ 表示总共有 $b$ 行、$y$ 列,且在上 $x$ 行只有右侧的 $a$ 列有 $1$ 的矩形。
那么观察一下可达的路径。
$(y\bmod x,y)$,$(x\bmod (y\bmod x),y+x-(y\bmod x))$,$((y\bmod x)\bmod(x\bmod (y\bmod x),y+x-(x\bmod (y\bmod x)))$。
不难注意到,上面这个过程其实就是辗转相除,最后的东西的 $b$ 肯定是小于 $x+y-1$ 的,且 $a=z$。
我们考虑随着 $m$ 的减少这玩意能少填的部分是什么,我们把某个 $(a_i,b_i)$ 能控制的列区间写出来。
不难发现 $b_i=x+y-a_{i-1}$。
$(a_i,b_i)$ 控制的区间是 $[b_i-a_i+1,m-a_i+1]$。
考虑相邻两个二元组在什么时候会开始减少、什么时候停止减少。
发现是在第 $i$ 项的尾等于下一项的头减一时也就是 $m-a_i+1=b_{i+1}-a_{i+1}$ 即 $m=x+y-1-a_{i+1}$ 时开始减少。
在第 $i+1$ 项变成空区间时也就是 $m-a_{i+1}+1=b_{i+1}-a_{i+1}$ 即 $m=x+y-{a_{i}}-1$ 时停止减少。
> 因为越靠后的二元组会越先变成空区间。
不难发现这玩意事实上就是在 $m\in[y,x+y-z-1]$ 时随着 $m$ 每减少 $1$ 多减少一列能控制的。
这个的变化是可以简单计算的。
#### 黄色部分
事实上如果我们令 $m\ge n$ 就没有影响,但是根据我们上面的式子会虚空减少(黄色矩形右边界小于左边界),减去即可,也是可以简单计算的。
## 算法三
不难发现横坐标和纵坐标在问题中是比较独立的,所以直接将 $x\times x$ 和 $y\times y$ 替换为 $a\times b$ 和 $c\times d$ 是没问题的。
> 再见了,各位。$\\$还在什么的,鸣泣之时里。