题解:CF2053G Naive String Splits
沉石鱼惊旋
·
·
题解
前言
这题太曲折了。最后的官方 Editorial 是我重写的。
https://codeforces.com/blog/entry/136455
并非本文抄袭官方题解,是官方题解抄袭本文。
题目翻译
给定长度为 n 的字符串 s 和长度为 m 的字符串 t。对于每个 k\in[1,n),问 s 的长度为 k 的前缀和 s 的长度为 n-k 的后缀这两个字符串,能不能拼接得到字符串 t。一个前缀 / 后缀可以使用多次。
多测,$1\leq T\leq 10^5$,$1\leq \sum m\leq 10^7$。
# 题目思路
不妨把前缀 $s_1$ 叫做短串,后缀 $s_2$ 叫做长串。如果 $|s_1|\gt |s_2|$ 换一下顺序不影响答案。
考虑一个贪心做法。我们每次先匹配几个短串,直到无法匹配。如果无法匹配,我们就尝试扔掉几个短串,放一个长串。枚举扔几个短串即可。**找到第一个位置使得可以放一个长串**。我们把这样放一次叫做一次『匹配过程』,每次『匹配过程』的开始位置就是上个『匹配过程』的下个位置。
但是这个做法是有漏洞的。下面将会说明这个漏洞的情况。
---
不难把长串看作是若干个短串拼上一个『尾巴』。
为什么只要找到第一个位置呢?为什么多反悔几个 $s_1$ 再放不会更优呢?
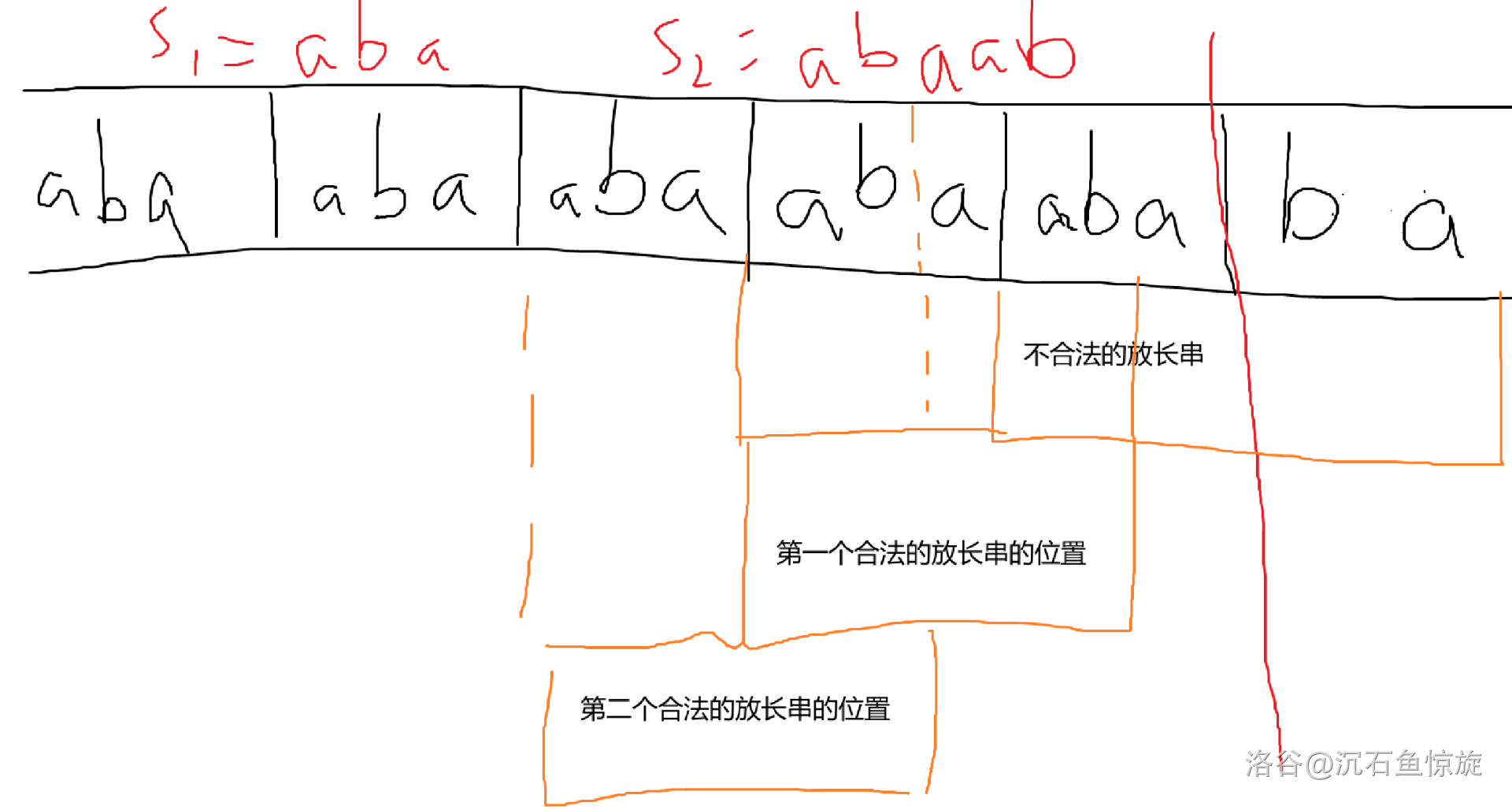
上图是一个例子。红线是我们匹配 $s_1$ 的截止位置。三个橙色方框表示尝试匹配长串的选择。
最后一个是不合法的,跳过,换『第一个合法的放长串的位置』这个框。这个框是合理的。
选第二个框和选第一个框的差距在,结束匹配进行下一轮的时候,我们需要匹配的内容,是选择了一段 $s_1$ 的后缀放到了 $s_1$ 的开头。
如图。
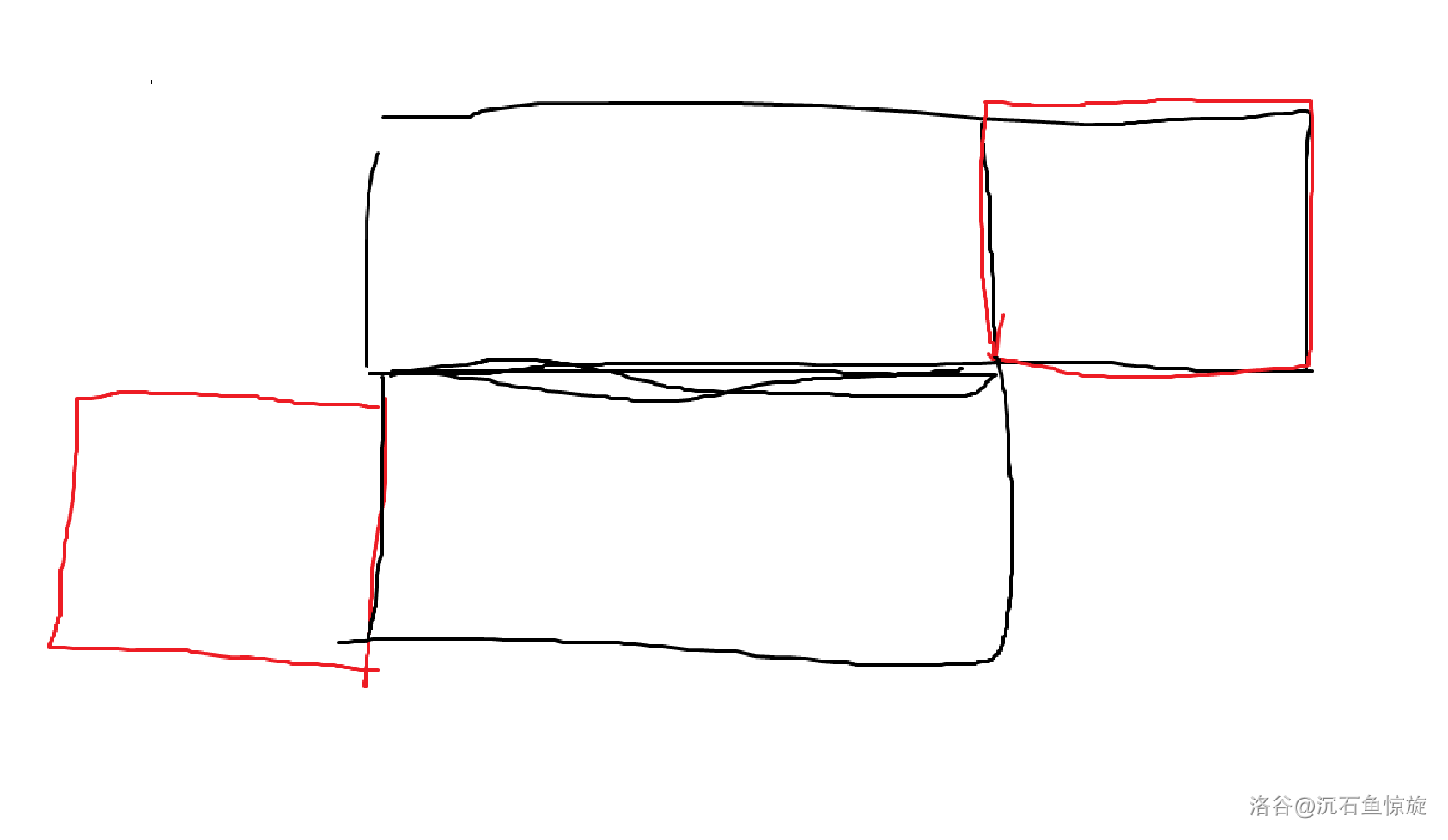
对齐得到下图。
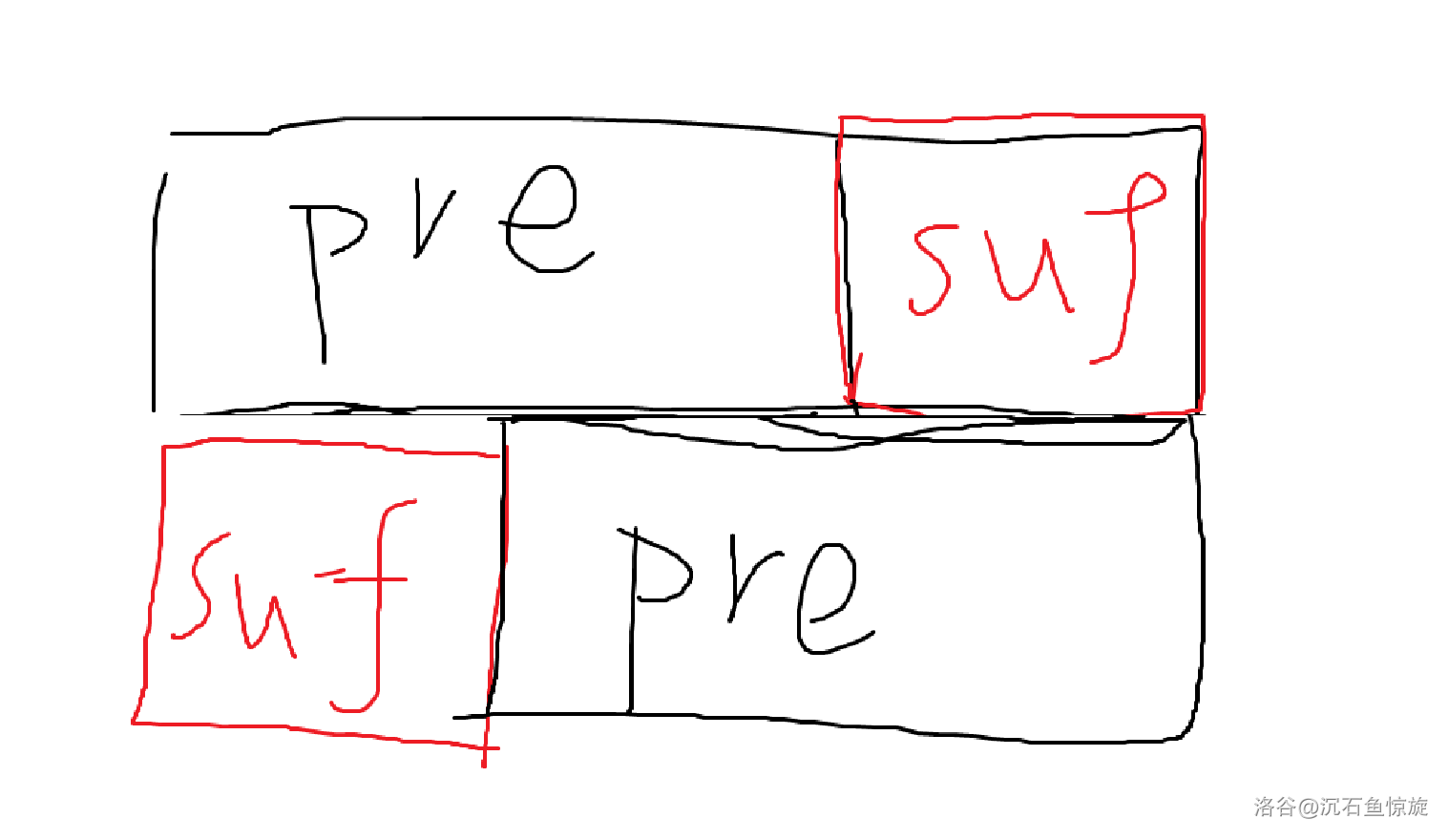
图中是 $|pre|\gt |suf|$ 的情况,另一种是同理的。
$pre+suf=suf+pre$,通过图片不难看出这里是 $pre+suf$ 需要“错位相等”的。也就是 $s_1$ 需要存在一个循环节,且『尾巴』也需要能够通过循环节拼出来,$s_2$ 前面那 $|s_1|$ 个字符还是需要能被循环节拼出来。
总结一下就是相当于 $s_1,s_2$ 有**公共循环节**。
也就是说,**反悔两次能凑出答案,反悔一次不一定可行**,需要满足二者有公共循环节。
有公共循环节这个太特殊了。首先这两个的公共循环节一定会是 $s$ 这个串的循环节。提前找到这个循环节,然后相当于是解方程,设 $a=|s_1|,b=|s_2|$,即判断是否有非负整数解 $x,y$ 满足 $xa+yb=|s|$。
这个解方程纯纯唬人。我们枚举 $y$,每一次计算枚举 $\mathcal O(\frac{m}{n})$ 次。最多 $n$ 次,复杂度 $\mathcal O(m)$。
---
漏洞解决了,剩下的情况我们**找到第一个可以放长串的位置就放**这个贪心是对的。
直接实现的话,复杂度最劣是调和级数的。考虑这个情况,$s_1=\texttt{a},s_2=\texttt{aaaaaaaab},t=\tt{aaaaaaaaaaaaaaaaaaaaaaaaab}$ 这种,我们尝试 $\mathcal O(\frac{m}{|s_1|})$ 步才能结束匹配短串。反悔每次至多 $\mathcal O(\frac{m}{|s_2|})$ 次,每次 $\mathcal O(\frac{|s_2|}{|s_1|})$。
---
好吧这个题确实是可以线性的。
首先设长串的前缀包含了 $c$ 个短串,那么我们反悔到的第一个『可以放长串的位置』只可能是反悔 $c$ 个短串或者 $c+1$ 个短串得到的。
这个很好理解,反悔 $c$ 个就是看作是长串的前缀,然后加上长串的『尾巴』。反悔 $c+1$ 个当且仅当长串的『尾巴』部分是短串的前缀。例如 CF 评论区的 hack:
<https://codeforces.com/blog/entry/136455?#comment-1234262>
```plain
1
8 8
abaabaab
abaababa
```
正确输出应该为
```plain
0010000
```
在 $k=3$ 的时候 $s_1=\texttt{aba},s_2=\texttt{abaab}$,此时我们先填充了 $2$ 个短串,但是只撤销 $c=1$ 个就会判成无解,std 的锅就是这么出的。只有在 $s_2$ 的『尾巴』部分是 $s_1$ 的前缀的时候才会出现这种情况。
所以我们每次计算的时候先二分出这个 $c$,复杂度是 $\mathcal O(\sum\limits_{i=1}^n\log(\frac n i))=\mathcal O(n)$ 的。之后反悔只需要进行两次判断。反悔过程做到线性了。
接下来对填充短串部分进行加速。暴力填充的 hack 上面已经给出了。如果直接使用一开始大家都认为是对的的『二分短串出现次数』的方法,那么可以通过
```plain
1
2 5000000
ab
abababab....abababab
```
这组 hack 卡到 $\log$。
@[_LHF_](/user/99506) 的评论指出两种替代方案。
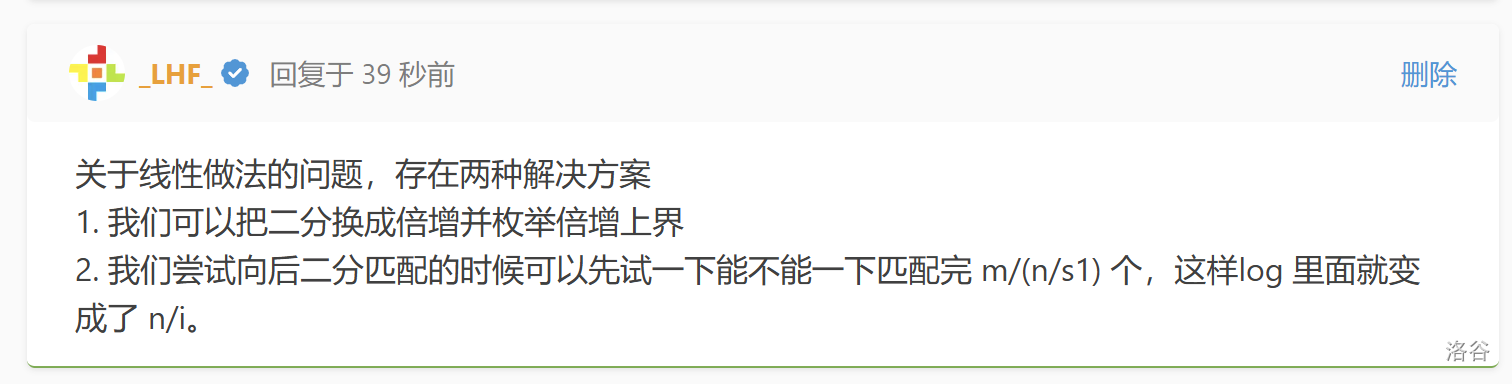
这里详细分析一下第二种做法。经过沟通,这里 lhf 老师笔误了。应该是匹配 $\frac{n}{|s_1|}$ 个。
类似分块,取 $B=\frac{n}{|s_1|}$。我们先尝试匹配 $B$ 个 $s_1$,也就是说每次匹配都可以往前推动 $n$ 个位置。之后剩下的部分不会超过 $B$ 个,二分出剩下内容具体有几个。而前面一次推进 $B$ 个的部分,至多反悔掉一次,后面二分,就变成了 $\mathcal O(\log B)$。每次至少可以填充 $|s_2|$ 个。这里计算一次答案复杂度就变成了 $\mathcal O(\frac{m}{|s_2|}\log B)$,总复杂度由于 $\mathcal O(\sum\limits_{i=1}^n\log(\frac n i))=\mathcal O(n)$ 所以是 $\mathcal O(m)$ 的。
至此,本题在线性时间解决了。
# 代码链接
这是一份依据 @[_LHF_](/user/99506) 指出的做法的第二条的实现。
[CF submission 299319348](https://codeforces.com/contest/2053/submission/299319348)