CF1012C Hills题解
linaonao
·
·
题解
这道题我们采用dp解决(纯贪心实在想不出来)
思路
于是$dp$所需的几个因素都被你考虑了,开始写公式(这里先出示公式,下面再讲解):
```cpp
f[i][j][0]=min(f[i-1][j][0],f[i-1][j][1]+max(0,a[i]-a[i-1]+1));
f[i][j][1]=min(f[i-2][j-1][0]+max(0,a[i-1]-a[i]+1),f[i-2][j-1][1]+max(0,max(a[i-1]-a[i]+1,a[i-1]-a[i-2]+1)));
```
第三维$0$表示不选,$1$选:
- 不选的情况由上一个选和不选推过来,注意**调整自身高度使满足上一个能做出贡献**。
- 选的情况,显然选了这一点,上一个点一定不选,于是我们从前一个点转移:
- 前一个点不选,就只需**调整上一个高度满足当前点能做出贡献**。
- 前一个点选,则**调整上一个点使前一个和当前一个都做出贡献**。
可以通过画图理解 (手画,丑,懂?) :
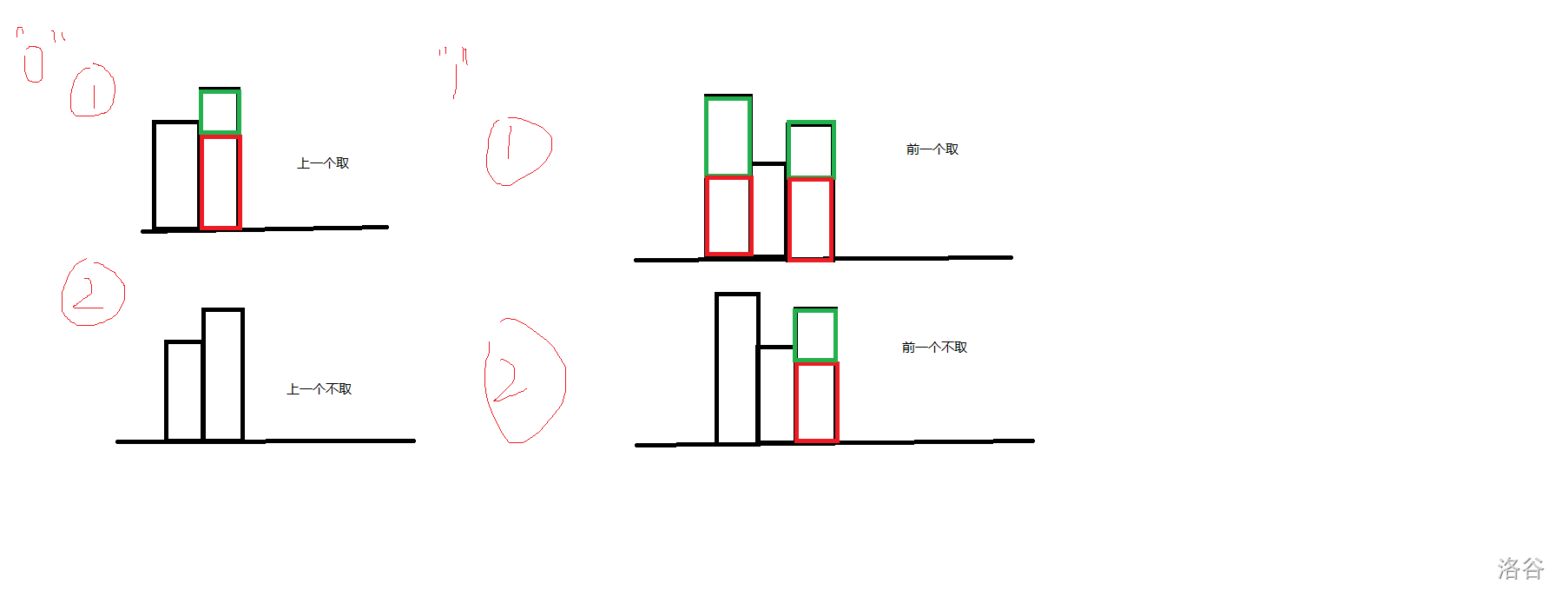
还有一个注意点,有可能**不需调整**,所以我们将代价与$0$取$max$。
最后贴上代码
~~~cpp
#include<bits/stdc++.h>
#define t(x) (x+1)/2
#define INF 0x3f3f3f
template<typename T>inline void read(T &x){
T f=0;x=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar())f|=ch=='-';
for(;isdigit(ch);ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
x=f?-x:x;
}
template<typename T>inline void write(T x){
if(x<0){putchar('-');x=-x;}
if(x>9)write(x/10);
putchar(x%10+48);
}
using namespace std;
int f[5005][5005][2];
int a[5005],n;
int main(){
read(n);
for(int i=1;i<=n;++i) read(a[i]);
a[0]=INF;
memset(f,INF,sizeof(f));
f[0][0][0]=0;f[1][0][0]=0;f[1][1][1]=0;
for(int i=2;i<=n;++i){
f[i][0][0]=f[i-1][0][0];
for(int j=1;j<=t(i);++j){
f[i][j][0]=min(f[i-1][j][0],f[i-1][j][1]+max(0,a[i]-a[i-1]+1));
f[i][j][1]=min(f[i-2][j-1][0]+max(0,a[i-1]-a[i]+1),f[i-2][j-1][1]+max(0,max(a[i-1]-a[i]+1,a[i-1]-a[i-2]+1)));
}
}
for(int i=1;i<=t(n);++i) printf("%d ",min(f[n][i][0],f[n][i][1]));
return 0;
}
~~~