P3690 动态树模板
有 n 个点,有点权。初始没有边,需要维护以下几个操作:
- 询问路径权值异或
- 在两点间连边,如果在一个联通块中则不连
- 删边,如果没有边则不删
- 改变一个点的权值
1 \leq n \leq 10^5$,$1 \leq m \leq 3 \times 10^5
动态树,又称 LCT,全称 Link-Cut-Tree
前芝知识:
- Splay
- 重链剖分
- 并查集
LCT 能干吗?
LCT 可以维护一个有根树森林,支持对树的分割(cut),合并(link)等操作的问题。
通俗地来讲:它支持以下操作:
- 查询两点之间路径上的信息(如和、异或和等)
- 连边
- 删边
- 动态维护连通性
LCT 怎么实现?
首先,学过重链剖分的应该知道,链剖分分为三类:重链剖分、实链剖分和长链剖分。它们的共同思想是把一棵树划分成若干条不相交的链,满足
- 每一个点恰好属于一条链
- 在同一条链中不存在深度相同的点
这样我们就可以把两点之间的路径转化为若干条链上的区间,可以大大减小操作次数。
关于重链剖分,实际上是根据子树的大小将每条边划分为“重边”和“轻边”,进而实现链剖分的。
关于长链剖分,由于没学过,我们也不敢乱说。
关于实链剖分,实际上是把每条边划分为“实边”和“虚边”。即你可以指定每个点一个“实儿子”,其它儿子为“虚儿子”,如果将每个点与它的实儿子连起来就可以形成实边,除实边之外的边是虚边,将实边连起来可以得到若干条实链。
区别于重链剖分的是每条边的虚实是可以动态变化的,而重链剖分,一旦遇到树的形态发生变化,就彻底萎了。
是不是听起来非常简单?不过,实链剖分最坏情况下还是 \mathcal O(n) 的,这样算上查询复杂度,就会变成 \mathcal O(n^2)!!!
不过,如果用强大的 \texttt{splay} 维护实链剖分,就可以得到均摊 \mathcal O(logn) 的 LCT。
我们对于每一个实链,建一棵 \texttt{splay} 里面包含所有这条链里的节点。这颗 \texttt{splay} 的中序遍历恰好按照这个链中每个节点的深度排序。即链顶(深度最小的点)位于中序遍历的第一位,链底(深度最大的点)位于中序遍历的最后一位。
当然,由于这棵树的完整性,我们只需建出一棵 \texttt{splay} 出来,具体见下方说明。
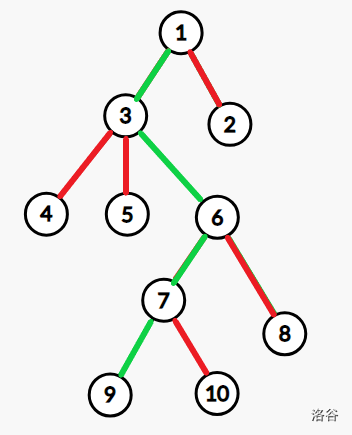
例如有一棵树如下图,根为 1:
那么我们就可以将它分成如下的链:(绿色表示实边,红色表示虚边):
这棵树中 6 条链分别是
-
\{1,2\}
-
\{3,6,8\}
-
\{4\}
-
\{5\}
-
\{7,9\}
-
\{10\}
那么我们考虑这样建 \texttt{splay}。
以路径 \{3,6,8\} 为例,节点 3 认一个父亲 1,但是 1 却不认这个儿子。他只有一个儿子 2。当然,2 也认这个父亲。
从此我们可以看出虚边只有儿子认父亲,父亲不认儿子。而实边儿子认父亲,父亲也认儿子。
上述图建成 \texttt{splay} 就是下图(一个手滑涂反了,绿色表示虚边,红色表示实边):
简单来说就是:一棵实子树表示一条链上的信息。例如 6 的实子树就表示了 3 \leftrightarrow 6 \leftrightarrow 8 这条链上的信息。
当然,除了实子树还有虚子树。通过观察我们可以发现 \texttt{splay} 中一个节点 x 的子树(不论虚实)包含了三个部分:
掌握了 \texttt{splay} 的构造,就要讲讲 LCT 的代码实现:
首先是节点信息与 pushup,学过 \texttt{splay} 的应该都不是太难理解:
struct node{
int f,ls,rs,val,sum;
} s[100005];
inline void pushup(int k){
s[k].sum=s[s[k].ls].sum^s[s[k].rs].sum^s[k].val;//维护子树异或和
}
接下来是 $identify$ 与 $connect$,$identify(x)$ 表示 $x$ 是 $x$ 的父亲的左儿子还是右儿子。与普通的 $\texttt{splay}$ 不同的一点是如果 $x$ 是当前所在 $\texttt{splay}$ 的根那么返回 $-1$。
```cpp
inline int identify(int k){
if(s[s[k].f].ls==k) return 0;
if(s[s[k].f].rs==k) return 1;
return -1;
}
inline void connect(int k,int f,int op){
s[k].f=f;
if(op==1) s[f].rs=k;
if(op==0) s[f].ls=k;
}
```
$rotate$ 与 $splay$ 函数,也有些不同:
```cpp
inline void rotate(int x){
int y=s[x].f;
int z=s[y].f;
int opy=identify(y);
int opx=identify(x);
int u=0;
if(opx==1) u=s[x].ls;
if(opx==0) u=s[x].rs;
connect(u,y,opx);
connect(y,x,opx^1);
connect(x,z,opy);
pushup(y);
pushup(x);
}
inline void splay(int k){
while(identify(k)!=-1){
register int up=s[k].f;
if(identify(up)==-1) rotate(k);
else if(identify(k)==identify(up)) rotate(up),rotate(k);
else rotate(k),rotate(k);
}
}
```
常规操作讲完了,接下来是 LCT 的重头戏:
$access(x)$:打通 $x$ 到整棵树的根节点(注意:不是 $x$ 所在的 $\texttt{splay}$ 的根节点)的路径并把它们打包成一个 $\texttt{splay}$,并自动把其他边设为虚边。
例如如果我们想打通 $10$ 到根的路径,那么这张图就变成了这样:
这时候我们想到了 $\texttt{splay}$ 的基础操作 $splay$,将一个点转到他所在的 $\texttt{splay}$ 的根节点(不要搞混淆,是**所在 $\texttt{splay}$ 的根节点**,跟之前那个不同)
我们从下往上跳(在这个例子中就是 $9 \rightarrow 7 \rightarrow 6 \rightarrow 3 \rightarrow 1$),我们先把 $9$ 旋转到所在 $\texttt{splay}$ 的根节点,然后把它的右儿子设为 $0$。由于我们把 $9$ 到根打包成一个 $\texttt{splay}$,所以原来 $9$ 的实儿子就变成了虚儿子。
同理,把 $7$ 旋转到它所在的 $\texttt{splay}$ 的根节点,然后将它的右儿子设为下一层节点 $9$。同理,把 $6$ 旋转到它所在的 $\texttt{splay}$ 的根节点,然后将它的右儿子设为下一层节点 $7$。以此类推就行了。
简单来说只有以下几步:
1. 转到 $\texttt{splay}$ 根节点
2. 改变右儿子的值,换为下一层节点
3. 更新信息
4. 往上跳
代码:
```cpp
inline void access(int k){
int l=0;
while(k){
splay(k);
s[k].rs=l;
pushup(k);
l=k;
k=s[k].f;
}
}
```
有了强大的 $access$ 操作,就可以引申出许多其它类型的操作了:
$makeroot(x)$:将 $x$ 号节点设为所在联通块的根。
首先打通 $x$ 到当前所在根节点的路径,那么此时 $x$ 一定是这个 $\texttt{splay}$ 中深度最大的,位于中序遍历的最后一位。
但是因为我们把它设为根节点(深度为 $0$),所以它就变为了这个 $\texttt{splay}$ 中深度最小的点。
同理,原本 $x$ 号节点的父亲应该是 $\texttt{splay}$ 中深度第二大的节点,即排在中序遍历的倒数第二位。现在经你这么一 $makeroot$,变成了 $x$ 的儿子,深度为 $1$,处于中序遍历的第二位。
想到了什么?
翻转。维护翻转的懒标记,记为 $lz$。
具体来说,就是打通 $x$ 到根的路径,把 $x$ 转到根节点,给 $x$ 打标记。
```cpp
struct node{
int f,ls,rs,val,sum,lz;
} s[100005];
inline void pushdown(int k){
if(s[k].lz){
swap(s[k].ls,s[k].rs);
if(s[k].ls) s[s[k].ls].lz^=1;
if(s[k].rs) s[s[k].rs].lz^=1;
s[k].lz=0;
}
}
inline void makeroot(int k){
access(k);
splay(k);
swap(s[k].ls,s[k].rs);//打标记
if(s[k].ls) s[s[k].ls].lz^=1;
if(s[k].rs) s[s[k].rs].lz^=1;
}
```
另外,在将一个节点旋转到根的时候,需要将根到 $x$ 的路径上所有点依次 $pushdown$,即下面的 $pushall$ 函数:
```cpp
inline void pushall(int x){
if(identify(x)!=-1) pushall(s[x].f);
pushdown(x);
}
```
并在 $splay$ 函数第一行加上
```cpp
pushall(k);
```
$split(x,y)$:把 $x - y$ 的路径拉成一个 $\texttt{splay}$。
有了 $makeroot$ 和 $access$,这个操作就显得轻而易举了。分别执行 $makeroot(x)$,$access(y)$,$splay(y)$ 三步就可以搞定了。
```cpp
inline void split(int x,int y){
makeroot(x);
access(y);splay(y);
}
```
$findroot(x)$:查找 $x$ 所在联通块的根
先打通 $x$ 到根节点的路径并把 $x$ 旋到 $\texttt{splay}$ 的根,由于根节点是这个 $\texttt{splay}$ 中深度最小的,所以我们就不停的往它的左儿子方向跳。注意每跳一步就 $pushdown$。
```cpp
inline int findroot(int k){
access(k);
splay(k);
while(s[k].ls) pushdown(k),k=s[k].ls;
splay(k);
return k;
}
```
$link(x,y)$:在 $x$ 与 $y$ 之间连边
类似并查集,判断是否在一个联通块。如果不在,就指定其中一个点的父亲为另一个点,即连一条虚边。
```cpp
inline void link(int x,int y){
makeroot(x);
if(findroot(y)==x) return;
s[x].f=y;
}
```
$cut(x,y)$:将 $(x,y)$ 边断开
这应该是比较难理解的操作了。
首先,需要判断 $x,y$ 是否在一个联通块。如果 $findroot(x) \neq findroot(y)$,那么直接跳出去。
否则,先把 $x-y$ 拉成一个 $\texttt{splay}$。由于在 $split$ 的代码中我们指定 $x$ 为联通块的根,$y$ 为 $\texttt{splay}$ 的根,因此 $x,y$ 之间有边当且仅当它们深度差为 $1$,即在 $\texttt{splay}$ 的中序遍历中相邻。这需要满足两个条件:
1. $x$ 的父亲为 $y$,因为一定是先访问 $y$ 的左儿子紧接着访问 $y$。
2. $x$ 不能有右子树。不然访问完 $x$ 之后一定会访问 $x$ 的右子树。
```cpp
inline bool cut(int x,int y){
if(findroot(x)!=findroot(y)) return 0;
split(x,y);
if(s[x].f!=y||s[x].rs) return 0;
s[x].f=s[y].ls=0;
pushup(x);
return 1;
}
```
查询操作:首先把 $x-y$ 拉成一个 $\texttt{splay}$,由于 LCT 中一个 $\texttt{splay}$ 的子树维护一条链上的信息,因此我们只需返回这个 $\texttt{splay}$ 的根节点,即 $y$ 号节点的 $sum$ 值就是结果。
模板题完整代码如下:
```cpp
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define foreach(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define all(a) a.begin(),a.end()
#define giveup(...) return printf(__VA_ARGS__),0;
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,0x3f,sizeof(a))
#define fillsmall(a) memset(a,0xcf,sizeof(a))
#define mask(a) (1ll<<(a))
#define maskx(a,x) ((a)<<(x))
#define _bit(a,x) (((a)>>(x))&1)
#define _sz(a) ((int)(a).size())
#define filei(a) freopen(a,"r",stdin);
#define fileo(a) freopen(a,"w",stdout);
#define fileio(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout)
#define eprintf(...) fprintf(stderr,__VA_ARGS__)
#define put(x) putchar(x)
#define eoln put('\n')
#define space put(' ')
#define y1 y_chenxiaoyan_1
#define y0 y_chenxiaoyan_0
typedef pair<int,int> pii;
inline int read(){
int x=0,neg=1;char c=getchar();
while(!isdigit(c)){
if(c=='-') neg=-1;
c=getchar();
}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
return x*neg;
}
inline void print(int x){
if(x<0){
putchar('-');
print(abs(x));
return;
}
if(x<=9) putchar(x+'0');
else{
print(x/10);
putchar(x%10+'0');
}
}
inline int qpow(int x,int e,int _MOD){
int ans=1;
while(e){
if(e&1) ans=ans*x%_MOD;
x=x*x%_MOD;
e>>=1;
}
return ans;
}
struct LCT{
struct node{
int f,ls,rs,val,sum,lz;
} s[100005];
inline void pushup(int k){
s[k].sum=s[s[k].ls].sum^s[s[k].rs].sum^s[k].val;
}
inline void pushdown(int k){
if(s[k].lz){
swap(s[k].ls,s[k].rs);
if(s[k].ls) s[s[k].ls].lz^=1;
if(s[k].rs) s[s[k].rs].lz^=1;
s[k].lz=0;
}
}
inline int identify(int k){
if(s[s[k].f].ls==k) return 0;
if(s[s[k].f].rs==k) return 1;
return -1;
}
inline void connect(int k,int f,int op){
s[k].f=f;
if(op==1) s[f].rs=k;
if(op==0) s[f].ls=k;
}
inline void rotate(int x){
int y=s[x].f;
int z=s[y].f;
int opy=identify(y);
int opx=identify(x);
int u=0;
if(opx==1) u=s[x].ls;
if(opx==0) u=s[x].rs;
connect(u,y,opx);
connect(y,x,opx^1);
connect(x,z,opy);
pushup(y);
pushup(x);
}
inline void pushall(int x){
if(identify(x)!=-1) pushall(s[x].f);
pushdown(x);
}
inline void splay(int k){
pushall(k);
while(identify(k)!=-1){
register int up=s[k].f;
// cout<<k<<" "<<up<<endl;
if(identify(up)==-1) rotate(k);
else if(identify(k)==identify(up)) rotate(up),rotate(k);
else rotate(k),rotate(k);
}
}
inline void access(int k){
int l=0;
while(k){
splay(k);
s[k].rs=l;
pushup(k);
l=k;
k=s[k].f;
}
}
inline void makeroot(int k){
access(k);
// puts("-1");
splay(k);
// puts("-1");
swap(s[k].ls,s[k].rs);
if(s[k].ls) s[s[k].ls].lz^=1;
if(s[k].rs) s[s[k].rs].lz^=1;
}
inline int findroot(int k){
access(k);
splay(k);
while(s[k].ls) pushdown(k),k=s[k].ls;
splay(k);
return k;
}
inline void split(int x,int y){
makeroot(x);
access(y);splay(y);
}
inline bool link(int x,int y){
makeroot(x);
if(findroot(y)==x) return 0;
s[x].f=y;
return 1;
}
inline bool cut(int x,int y){
if(findroot(x)!=findroot(y)) return 0;
split(x,y);
if(s[x].f!=y||s[x].rs) return 0;
s[x].f=s[y].ls=0;
pushup(x);
return 1;
}
} lct;
int n=read(),m=read();
signed main(){
fz(i,1,n) lct.s[i].val=read(),lct.s[i].sum=lct.s[i].val;
fz(i,1,m){
int opt=read(),x=read(),y=read();
if(opt==0) lct.split(x,y),cout<<lct.s[y].sum<<endl;
if(opt==1) lct.link(x,y);
if(opt==2) lct.cut(x,y);
if(opt==3) lct.splay(x),lct.s[x].val=y;
}
return 0;
}
```
创作声明:
部分内容借鉴了 FlashHu 的题解
~~写题解不容易,快快点个赞呗~~