（2021.8.15 更新）洛谷主题库试题提供以及反馈帖

工单反馈版

chen_zhe @ 2020-01-19 19:25:41

洛谷鼓励各位用户将大型比赛的试题或者洛谷上缺乏的模板题，在确认没有版权问题的情况下，提供给洛谷。但是因为此类贴子日益增多，严重影响了讨论版面，而且部分用户所提供的试题并不符合规定，故做出以下说明：

  • 所谓的大型比赛，指的是国家或者地区级别的比赛（例如 USACO，POI，Baltic OI 等），或者大型的网络公开赛（例如 Codeplus 等），但是不包含例如校内的网络模拟赛之类的试题。
  • 请注意，JOI 有关竞赛（包括 JOI open）原则上是不接受用户投题的。对于其它大型竞赛题目，如果测试点过多且单个测试点时间过长也有被拒绝的可能。如果您希望搬运这类比赛题，请提前咨询管理员。另外 USACO 的铜组也不接受用户投题。
  • 对于模板题，其在现在的 OI 中，必须存在一定的实际意义，不能是非常生僻的，全网可能没有一个算法竞赛题涉及到相关知识点的算法或者数据结构。洛谷现决定根据 OI-Wiki 判断一个模板是否有存在的必要，即必须在 OI-Wiki 中有一个专门的页面。对于以前不符合此项要求的模板题，取消模板标签。同时，建议在造模板题之前先与管理员私信沟通好洛谷是否接受该模板。
  • 贡献大型比赛的试题必须确保没有版权争议。为防止出现版权问题导致的不必要纠纷，供题时必须标注题目来源，搬运题目必须标注原题链接。若需搬运来自其他 Online Judge 的翻译题，必须确保没有任何版权问题的情况下，按照洛谷主题库题目规范所要求的格式以及对方 Online Judge 的版权要求进行搬运。若贡献明显有版权问题的题目，视情节严重程度处以警告/禁言/棕名/封号的惩罚。另外，对于比赛赛题，请一次性提交一场比赛中所有的题目。只有在题库中相应比赛的题目出现缺漏的时候才允许零散提交。特殊地，对于 COCI 题目，如果题库中只缺失 AB 两题，从现在起不再接受补充，但是对于整套提供的题目，仍然接受前两题。
  • 贡献的题目需严格遵守洛谷主题库题目规范，请在贡献之前对照规范逐字逐句检查。特别地，所提供的试题中，若需要 spj，则相对较易的部分必须自行完成。若实在有困难才可以征集。具体尺度由管理进行评判。
  • 在本讨论中，允许用户提供试题，要求用户至少达到绿勾级别。
  • 贡献题目禁止单独开帖，请在此讨论下回复，若恶意浪费管理员时间，视情节严重程度处以警告/禁言/封号的惩罚。
  • 原则上不收距今超过 20 年（含）的题目，如果题目具有特殊价值，可以联系管理员添加单题（而不是整套提供）

同时，对于已在洛谷主题库中但不符合洛谷主题目题目规范的题目，我们鼓励用户进行更正，但也至少要达到绿勾级别。要求更正后的题面严格遵守规范，同样回复在本讨论下，为了方便管理员，请将题面使用代码框```括起来。

若有发现难度标签明显有问题（即对于普及-以及以下的题目相差两个档次，或者对于提高-以及以上难度相差一个档次），欢迎大家提供建议。请在本楼回复题号和应当修正的难度。

为了提高管理员的审核效率，本贴禁止任何无意义回复，所有无意义回复均会被删除，行为恶劣者将会禁言，但是可以询问说明中的问题。若为修复题目问题，建议带上链接以增加效率。

请不要@管理员，会有管理员不定期来本帖处理。

by 一扶苏一 @ 2020-01-27 17:44:03

类型：题面修改

题目：P3690

理由：原题的样例有些过于弱了，根据洛谷的题目题目规范，样例应该具有一定强度并囊括所有可能出现的操作。因此提供一个强度适中调试方便的新样例，望予增加。

Sample Input

5 14
114 514 19 19 810
1 1 2
0 1 2
2 1 2
1 1 2
1 2 3
2 1 3
1 1 3
1 4 5
1 2 5
0 3 5
0 3 4
3 5 233333
0 1 5
0 2 5

Sample Output

624
315
296
232709
232823

by syksykCCC @ 2020-01-27 20:37:35

类型：题面修改

题目：P5043 【模板】树同构

其实问题不大，但空格、数据范围的 \% 等不符合规范……

新题面：

## 题目描述

树是一种很常见的数据结构。

我们把 $N$ 个点，$N-1$ 条边的连通无向图称为树。

若将某个点作为根，从根开始遍历，则其它的点都有一个前驱，这个树就成为有根树。

对于两个树 $T_1$ 和 $T_2$，如果能够把树 $T_1$ 的所有点重新标号，使得树 $T_1$ 和树 $T_2$ 完全相同，那么这两个树是同构的。也就是说，它们具有相同的形态。

现在，给你 $M$ 个有根树，请你把它们按同构关系分成若干个等价类。

## 输入格式

第一行，一个整数 $M$。

接下来 $M$ 行，每行包含若干个整数，表示一个树。第一个整数 $N$表示点数。接下来 $N$ 个整数，依次表示编号为 $1$ 到 $N$ 的每个点的父亲结点的编号。根节点父亲结点编号为 $0$。

## 输出格式

输出 $M$ 行，每行一个整数，表示与每个树同构的树的最小编号。

## 说明/提示

编号为 $1, 2, 4$ 的树是同构的。编号为 $3$ 的树只与它自身同构。

对于 $100\%$ 的数据，$1\leq N,M\leq 50$。

题目描述

树是一种很常见的数据结构。

我们把 N 个点，N-1 条边的连通无向图称为树。

若将某个点作为根，从根开始遍历，则其它的点都有一个前驱，这个树就成为有根树。

对于两个树 T_1 和 T_2，如果能够把树 T_1 的所有点重新标号，使得树 T_1 和树 T_2 完全相同，那么这两个树是同构的。也就是说，它们具有相同的形态。

现在，给你 M 个有根树，请你把它们按同构关系分成若干个等价类。

输入格式

第一行，一个整数 M。

接下来 M 行，每行包含若干个整数，表示一个树。第一个整数 N表示点数。接下来 N 个整数，依次表示编号为 1 到 N 的每个点的父亲结点的编号。根节点父亲结点编号为 0。

输出格式

输出 M 行，每行一个整数，表示与每个树同构的树的最小编号。

说明/提示

编号为 1, 2, 4 的树是同构的。编号为 3 的树只与它自身同构。

对于 100\% 的数据，1\leq N,M\leq 50。

by syksykCCC @ 2020-01-27 21:18:28

类型：题面修改

题目：P1445 [Violet]樱花

原题题面实在辣眼，在不影响题意的情况下稍作了修改。

新题面：

## 题目描述

求方程：

$$\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{n!}$$ 

的正整数解的组数，答案模 $10^9+7$。

## 输入格式

输入一个正整数 $n$。

## 输出格式

输出答案，正整数解的组数模 $10^9+7$ 的值。

## 说明/提示

对于 $100\%$ 的数据，$1 \le n \le 10^6$。

题目描述

求方程：

\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{n!}

的正整数解的组数，答案模 10^9+7。

输入格式

输入一个正整数 n。

输出格式

输出答案，正整数解的组数模 10^9+7 的值。

说明/提示

对于 100\% 的数据，1 \le n \le 10^6。

by HohleFeuerwerke @ 2020-01-28 11:40:31

@StudyingFather 不好意思之前一直在水犇犇。

我记得那题好像可以快速幂卡过去的？？？

所以出了一道卡快速幂的。

by tzc_wk @ 2020-01-28 13:48:48

类型：试题提供

题目：[【模板】最大权闭合子图](https://www.luogu.com.cn/problem/U103816)

by Leasier @ 2020-01-28 14:43:59

类型：模板题提供

题目：【模板】Miller-Rabin

by tzc_wk @ 2020-01-28 17:35:57

管理员大人请尽快审核我今天和昨天的申请啊！

by 　　　吾皇 @ 2020-01-28 19:56:27

类型：题面修改

题目： [APIO2007]动物园

新题面：

### 题目描述
新建的圆形动物园是亚太地区的骄傲。圆形动物园坐落于太平洋的一个小岛上，包含一大圈围栏，每个围栏里有一
种动物。如下图所示：

![](https://cdn.luogu.com.cn/upload/image_hosting/8pr43p86.png)

你是动物园的公共主管。你要做的是，让每个来动物园的人都尽可能高兴。今天有一群小朋友来动物园参观，你希望能让他们在动物园度过一段美好的时光。但这并不是一件容易的事——有的动物有一些小朋友喜欢，有的动物有一些小朋友害怕。如，Alex 喜欢可爱的猴子和考拉，而害怕拥牙齿锋利的狮子。而Polly 会因狮子有美丽的鬃毛而喜欢它，但害怕有臭味的考拉。你可以选择将一些动物从围栏中移走以使得小朋友不会害怕。但你不能移走所有的动物，否则小朋友们就没有动物可看了。每个小朋友站在大围栏圈的外面，可以看到连续的 $5$ 个围栏。你得到了所有小朋友喜欢和害怕的动物信息。当下面两处情况之一发生时，小朋友就会高兴：
- 至少有一个他害怕的动物被移走
- 至少有一个他喜欢的动物没被移走

例如，考虑下图中的小朋友和动物：

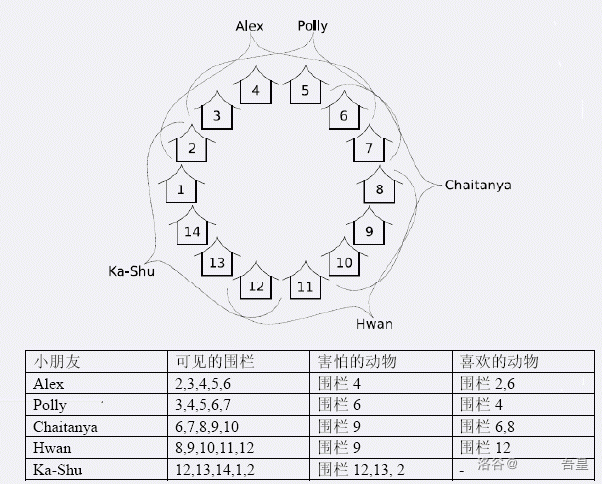
![](https://cdn.luogu.com.cn/upload/image_hosting/n69iqfv6.png)

- 假如你将围栏 $4$ 和 $12$ 的动物移走。Alex 和 Ka-Shu 将很高兴，因为至少有一个他们害怕的动物被移走了。这也会使 Chaitanya 高兴，因为他喜欢的围栏  $6$ 和 $8$ 中的动物都保留了。但是，Polly 和 Hwan 将不高兴，因为他们看不到任何他们喜欢的动物，而他们害怕的动物都还在。这种安排方式使得三个小朋友高兴。
- 现在，换一种方法，如果你将围栏 $4$ 和 $6$ 中的动物移走，Alex 和 Polly 将很高兴，因为他们害怕的动物被移走了。Chaitanya 也会高兴，虽然他喜欢的动物 $6$ 被移走了，他仍可以看到围栏 $8$ 里面他喜欢的动物。同样的 Hwan 也会因可以看到自己喜欢的动物 $12$ 而高兴。唯一不高兴的只有 Ka-Shu。
- 如果你只移走围栏 $13$ 中的动物，Ka-Shu 将高兴，因为有一个他害怕的动物被移走了，Alex, Polly, Chaitanya 和 Hwan 也会高兴，因为他们都可以看到至少一个他们喜欢的动物。所以有 $5$ 个小朋友会高兴。这种方法使得了最多的小朋友高兴。

### 输入格式
- 输入的第一行包含两个整数 $N$，$C$，用空格分隔。

$N$ 是围栏数（$10 \le N \le 10^4$），$C$ 是小朋友的个数（$1 \le C \le 5\times 10^4$）。

围栏按照顺时针的方向编号为 $1,2,3,\cdots,N$。

- 接下来的 $C$ 行，每行描述一个小朋友的信息，以下面的形式给出： $E, F, L ,X_1, X_2 ,\cdots ,X_F ,Y_1 ,Y2 ,\cdots ,Y_L$。 

其中： $E$ 表示这个小朋友可以看到的第一个围栏的编号（$1 \le E \le N$），换句话说，该小朋友可以看到的围栏为 $E$， $E+1$， $E+2$， $E+3$， $E+4$。

注意，如果编号超过 $N$ 将继续从 $1$ 开始算。

如：当 $N=14$，$ E=13$ 时，这个小朋友可以看到的围栏为 $13,14,1, 2$ 和 $3$。

$F$ 表示该小朋友害怕的动物数。

$L$ 表示该小朋友喜欢的动物数。

围栏 $X_1, X_2, \cdots, X_F$ 中包含该小朋友害怕的动物。

围栏 $Y1, Y2, \cdots, Y_L$ 中包含该小朋友喜欢的动物。 

$X_1, X_2, \cdots, X_F, Y_1, Y_2, \cdots, Y_L$ 是两两不同的整数，而且所表示的围栏都是该小朋友可以看到的。

小朋友已经按照他们可以看到的第一个围栏的编号从小到大的顺序排好了（这样最小的 $E$ 对应的小朋友排在第一个，最大的 $E$ 对应的小朋友排在最后一个）。

注意可能有多于一个小朋友对应的 $E$ 是相同的。

### 输出格式
仅输出一个数，表示最多可以让多少个小朋友高兴。

### 说明/提示

**数据范围**
对于 $100\%$ 的数据，$10 \le N \le 10^4$，$1 \le C \le 5\times 10^4$，$1 \le E \le N$。

**样例说明**
- 第一个样例是题目描述中的例子，所有的 $C=5$ 个小朋友都能高兴。
- 第二个样例是一个不能使得所有 $C=7$ 个小朋友都高兴的例子。

题目描述

新建的圆形动物园是亚太地区的骄傲。圆形动物园坐落于太平洋的一个小岛上，包含一大圈围栏，每个围栏里有一 种动物。如下图所示：

你是动物园的公共主管。你要做的是，让每个来动物园的人都尽可能高兴。今天有一群小朋友来动物园参观，你希望能让他们在动物园度过一段美好的时光。但这并不是一件容易的事——有的动物有一些小朋友喜欢，有的动物有一些小朋友害怕。如，Alex 喜欢可爱的猴子和考拉，而害怕拥牙齿锋利的狮子。而Polly 会因狮子有美丽的鬃毛而喜欢它，但害怕有臭味的考拉。你可以选择将一些动物从围栏中移走以使得小朋友不会害怕。但你不能移走所有的动物，否则小朋友们就没有动物可看了。每个小朋友站在大围栏圈的外面，可以看到连续的 5 个围栏。你得到了所有小朋友喜欢和害怕的动物信息。当下面两处情况之一发生时，小朋友就会高兴：

例如，考虑下图中的小朋友和动物：

输入格式

围栏按照顺时针的方向编号为 $1,2,3,\cdots,N$。 - 接下来的 $C$ 行，每行描述一个小朋友的信息，以下面的形式给出： $E, F, L ,X_1, X_2 ,\cdots ,X_F ,Y_1 ,Y2 ,\cdots ,Y_L$。 其中： $E$ 表示这个小朋友可以看到的第一个围栏的编号（$1 \le E \le N$），换句话说，该小朋友可以看到的围栏为 $E$， $E+1$， $E+2$， $E+3$， $E+4$。 注意，如果编号超过 $N$ 将继续从 $1$ 开始算。 如：当 $N=14$，$ E=13$ 时，这个小朋友可以看到的围栏为 $13,14,1, 2$ 和 $3$。 $F$ 表示该小朋友害怕的动物数。 $L$ 表示该小朋友喜欢的动物数。 围栏 $X_1, X_2, \cdots, X_F$ 中包含该小朋友害怕的动物。 围栏 $Y1, Y2, \cdots, Y_L$ 中包含该小朋友喜欢的动物。 $X_1, X_2, \cdots, X_F, Y_1, Y_2, \cdots, Y_L$ 是两两不同的整数，而且所表示的围栏都是该小朋友可以看到的。 小朋友已经按照他们可以看到的第一个围栏的编号从小到大的顺序排好了（这样最小的 $E$ 对应的小朋友排在第一个，最大的 $E$ 对应的小朋友排在最后一个）。 注意可能有多于一个小朋友对应的 $E$ 是相同的。 ### 输出格式 仅输出一个数，表示最多可以让多少个小朋友高兴。 ### 说明/提示 **数据范围** 对于 $100\%$ 的数据，$10 \le N \le 10^4$，$1 \le C \le 5\times 10^4$，$1 \le E \le N$。 **样例说明** - 第一个样例是题目描述中的例子，所有的 $C=5$ 个小朋友都能高兴。 - 第二个样例是一个不能使得所有 $C=7$ 个小朋友都高兴的例子。

by Hexarhy @ 2020-01-28 23:21:24

类型：题面修改

题目：P1901 发射站

修改内容（剪贴板）

by Froggy @ 2020-01-29 10:31:25

贡献题目：

[SDOI2012]走迷宫

上一页 | 下一页