（2021.8.15 更新）洛谷主题库试题提供以及反馈帖

工单反馈版

chen_zhe @ 2020-01-19 19:25:41

洛谷鼓励各位用户将大型比赛的试题或者洛谷上缺乏的模板题，在确认没有版权问题的情况下，提供给洛谷。但是因为此类贴子日益增多，严重影响了讨论版面，而且部分用户所提供的试题并不符合规定，故做出以下说明：

所谓的大型比赛，指的是国家或者地区级别的比赛（例如 USACO，POI，Baltic OI 等），或者大型的网络公开赛（例如 Codeplus 等），但是不包含例如校内的网络模拟赛之类的试题。
请注意，JOI 有关竞赛（包括 JOI open）原则上是不接受用户投题的。对于其它大型竞赛题目，如果测试点过多且单个测试点时间过长也有被拒绝的可能。如果您希望搬运这类比赛题，请提前咨询管理员。另外 USACO 的铜组也不接受用户投题。
对于模板题，其在现在的 OI 中，必须存在一定的实际意义，不能是非常生僻的，全网可能没有一个算法竞赛题涉及到相关知识点的算法或者数据结构。洛谷现决定根据 OI-Wiki 判断一个模板是否有存在的必要，即必须在 OI-Wiki 中有一个专门的页面。对于以前不符合此项要求的模板题，取消模板标签。同时，建议在造模板题之前先与管理员私信沟通好洛谷是否接受该模板。
贡献大型比赛的试题必须确保没有版权争议。为防止出现版权问题导致的不必要纠纷，供题时必须标注题目来源，搬运题目必须标注原题链接。若需搬运来自其他 Online Judge 的翻译题，必须确保没有任何版权问题的情况下，按照洛谷主题库题目规范所要求的格式以及对方 Online Judge 的版权要求进行搬运。若贡献明显有版权问题的题目，视情节严重程度处以警告/禁言/棕名/封号的惩罚。另外，对于比赛赛题，请一次性提交一场比赛中所有的题目。只有在题库中相应比赛的题目出现缺漏的时候才允许零散提交。特殊地，对于 COCI 题目，如果题库中只缺失 AB 两题，从现在起不再接受补充，但是对于整套提供的题目，仍然接受前两题。
贡献的题目需严格遵守洛谷主题库题目规范，请在贡献之前对照规范逐字逐句检查。特别地，所提供的试题中，若需要 spj，则相对较易的部分必须自行完成。若实在有困难才可以征集。具体尺度由管理进行评判。
在本讨论中，允许用户提供试题，要求用户至少达到绿勾级别。
贡献题目禁止单独开帖，请在此讨论下回复，若恶意浪费管理员时间，视情节严重程度处以警告/禁言/封号的惩罚。
原则上不收距今超过 20 年（含）的题目，如果题目具有特殊价值，可以联系管理员添加单题（而不是整套提供）

同时，对于已在洛谷主题库中但不符合洛谷主题目题目规范的题目，我们鼓励用户进行更正，但也至少要达到绿勾级别。要求更正后的题面严格遵守规范，同样回复在本讨论下，为了方便管理员，请将题面使用代码框```括起来。

若有发现难度标签明显有问题（即对于普及-以及以下的题目相差两个档次，或者对于提高-以及以上难度相差一个档次），欢迎大家提供建议。请在本楼回复题号和应当修正的难度。

为了提高管理员的审核效率，本贴禁止任何无意义回复，所有无意义回复均会被删除，行为恶劣者将会禁言，但是可以询问说明中的问题。若为修复题目问题，建议带上链接以增加效率。

请不要@管理员，会有管理员不定期来本帖处理。

by Monkey_Hunter @ 2020-02-15 15:42:01

@Alpha 代码框

by Smile_Cindy @ 2020-02-15 16:16:54

题目描述

有 N 家洗车店从左往右排成一排，每家店都有一个正整数价格 P_i 。有 M 个人要来消费，第i个人会驶过第 A_i 个开始一直到第 B_i 个洗车店，且会选择这些店中最便宜的一个进行一次消费。但是如果这个最便宜的价格大于 C_i ，那么这个人就不洗车了。请给每家店指定一个价格，使得所有人花的钱的总和最大。

输入格式

第一行包含两个正整数 N,M (1\le N\le 50,1\le M \le 4000) 。接下来 M 行，每行包含三个正整数 A_i,B_i,C_i 。

输出格式

第一行输出一个正整数，即消费总额的最大值。第二行输出 N 个正整数，依次表示每家洗车店的价格 P_i ，要求 1\le P_i\le 500000 。若有多组最优解，输出任意一组。

说明/提示

无（原题说明提示和题目描述重了）

## 题目描述

有 $N$ 家洗车店从左往右排成一排，每家店都有一个正整数价格 $P_i$ 。有 $M$ 个人要来消费，第i个人会驶过第 $A_i$ 个开始一直到第 $B_i$ 个洗车店，且会选择这些店中最便宜的一个进行一次消费。但是如果这个最便宜的价格大于 $C_i$ ，那么这个人就不洗车了。请给每家店指定一个价格，使得所有人花的钱的总和最大。

## 输入格式

第一行包含两个正整数 $N,M (1\le N\le 50,1\le M \le 4000)$ 。接下来 $M$ 行，每行包含三个正整数 $A_i,B_i,C_i$ 。

## 输出格式

第一行输出一个正整数，即消费总额的最大值。第二行输出 $N$ 个正整数，依次表示每家洗车店的价格 $P_i$ ，要求 $1\le P_i\le 500000$ 。若有多组最优解，输出任意一组。

## 说明/提示

无（原题说明提示和题目描述重了）

by Smile_Cindy @ 2020-02-15 16:18:04

重发P3592 题面修改

by Smile_Cindy @ 2020-02-15 16:22:22

重发P3353题面修改：

鉴于题面太长，从“现在问题来了”开始：

现在问题来了：天空可以理解为一条数轴，在这条数轴上分布着许多颗星星，对于每颗星星都有它的位置 x_i 和自身的亮度 b_i 。而窗户所能看到的范围是一个给出的参数 W ，我们看到的星星也包括窗户边缘的星星。现在，要你求出调整窗户位置后能看到星星的亮度之和最大值。

输入格式第一行两个整数 N,W ，分别代表星星的数量和窗户的宽度

第二行到第 N+1 行，第 i+1 行输入两个整数 x_i,b_i 分别代表星星的坐标和亮度。

数据范围对于 10\% 的数据，W=0（没有边缘）

对于 40\% 的数据，W \le 1000

对于100%的数据，N\le 10^5，W\le 10^5，x_i\le 10^5，b_i\le 100

除 W=0 的情况外，W\ge 3 且为奇数

现在问题来了：天空可以理解为一条数轴，在这条数轴上分布着许多颗星星，对于每颗星星都有它的位置 $x_i$ 和自身的亮度 $b_i$ 。而窗户所能看到的范围是一个给出的参数 $W$ ，我们看到的星星也包括窗户边缘的星星。现在，要你求出调整窗户位置后能看到星星的亮度之和最大值。

输入格式
第一行两个整数 $N,W$ ，分别代表星星的数量和窗户的宽度

第二行到第 $N+1$ 行，第 $i+1$ 行输入两个整数 $x_i,b_i$ 分别代表星星的坐标和亮度。

数据范围
对于 $10\%$ 的数据，$W=0$（没有边缘）

对于 $40\%$ 的数据，$W \le 1000$

对于100%的数据，$N\le 10^5$，$W\le 10^5$，$x_i\le 10^5$，$b_i\le 100$

除 $W=0$ 的情况外，$W\ge 3$ 且为奇数

by Smile_Cindy @ 2020-02-15 16:22:31

@mrsrz

by Itst @ 2020-02-15 19:13:02

类型：题面修改

题目：NOI2005 月下柠檬树

新题面：

### 题目描述

李哲非常非常喜欢柠檬树，特别是在静静的夜晚，当天空中有一弯明月温柔地照亮地面上的景物时，他必会悠闲地坐在他亲手植下的那棵柠檬树旁，独自思索着人生的哲理。

李哲是一个喜爱思考的孩子，当他看到在月光的照射下柠檬树投在地面上的影子是如此的清晰，马上想到了一个问题：树影的面积是多大呢？

李哲知道，直接测量面积是很难的，他想用几何的方法算，因为他对这棵柠檬树的形状了解得非常清楚，而且想好了简化的方法。

李哲将整棵柠檬树分成了 $n$ 层，由下向上依次将层编号为 $1,2,...,n$。从第 $1$ 到 $n-1$ 层，每层都是一个圆台型，第 $n$ 层(最上面一层)是圆锥型。对于圆台型， 其上下底面都是水平的圆。对于相邻的两个圆台，上层的下底面和下层的上底面重合。第 $n$ 层(最上面一层)圆锥的底面就是第 $n-1$ 层圆台的上底面。所有的底面 的圆心(包括树顶)处在同一条与地面垂直的直线上。李哲知道每一层的高度为 $h_1,h_2,...,h_n$，第 $1$ 层圆台的下底面距地面的高度为 $h_0$，以及每层的下底面的圆的半径 $r_1,r_2,...,r_n$。李哲用熟知的方法测出了月亮的光线与地面的夹角为 $\mathrm{alpha}$。

![](https://cdn.luogu.com.cn/upload/pic/13770.png)

为了便于计算，假设月亮的光线是平行光，且地面是水平的，在计算时忽略树干所产生的影子。李哲当然会算了，但是他希望你也来练练手。

### 输入格式

第一行包含一个整数 $n$ 和一个实数 $\mathrm{alpha}$，表示柠檬树的层数和月亮 的光线与地面夹角（单位为弧度）。

第二行包含 $n+1$ 个实数 $h_0,h_1,h_2,...,h_n$ 表示树离地的高度和每层的高度。

第三行包含 $n$ 个实数 $r_1,r_2,...,r_n$ 表示柠檬树每层下底面的圆的半径。

同一行相邻的两个数之间用一个空格分隔。

输入的所有实数的小数点后可能包含一至十位有效数字。

### 输出格式

输出一个实数，表示树影的面积，四舍五入保留两位小数。

### 数据范围

对于 $10 \%$ 的数据，$n \leq 1$；

对于 $30 \%$ 的数据，$n \leq 2$；

对于 $60 \%$ 的数据，$n \leq 20$；

对于 $100 \%$ 的数据，$1 \leq n \leq 500$，$0.3 < \mathrm{alpha} < \frac{\pi}{2}$，$0 < h_i \leq 100$，$0 < r_i \leq 100$。

题目描述

李哲非常非常喜欢柠檬树，特别是在静静的夜晚，当天空中有一弯明月温柔地照亮地面上的景物时，他必会悠闲地坐在他亲手植下的那棵柠檬树旁，独自思索着人生的哲理。

李哲是一个喜爱思考的孩子，当他看到在月光的照射下柠檬树投在地面上的影子是如此的清晰，马上想到了一个问题：树影的面积是多大呢？

李哲知道，直接测量面积是很难的，他想用几何的方法算，因为他对这棵柠檬树的形状了解得非常清楚，而且想好了简化的方法。

李哲将整棵柠檬树分成了 n 层，由下向上依次将层编号为 1,2,...,n。从第 1 到 n-1 层，每层都是一个圆台型，第 n 层(最上面一层)是圆锥型。对于圆台型，其上下底面都是水平的圆。对于相邻的两个圆台，上层的下底面和下层的上底面重合。第 n 层(最上面一层)圆锥的底面就是第 n-1 层圆台的上底面。所有的底面的圆心(包括树顶)处在同一条与地面垂直的直线上。李哲知道每一层的高度为 h_1,h_2,...,h_n，第 1 层圆台的下底面距地面的高度为 h_0，以及每层的下底面的圆的半径 r_1,r_2,...,r_n。李哲用熟知的方法测出了月亮的光线与地面的夹角为 \mathrm{alpha}。

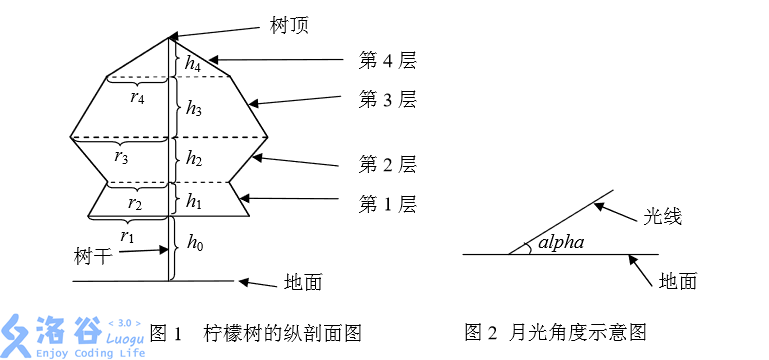
为了便于计算，假设月亮的光线是平行光，且地面是水平的，在计算时忽略树干所产生的影子。李哲当然会算了，但是他希望你也来练练手。

输入格式

第一行包含一个整数 n 和一个实数 \mathrm{alpha}，表示柠檬树的层数和月亮的光线与地面夹角（单位为弧度）。

第二行包含 n+1 个实数 h_0,h_1,h_2,...,h_n 表示树离地的高度和每层的高度。

第三行包含 n 个实数 r_1,r_2,...,r_n 表示柠檬树每层下底面的圆的半径。

同一行相邻的两个数之间用一个空格分隔。

输入的所有实数的小数点后可能包含一至十位有效数字。

输出格式

输出一个实数，表示树影的面积，四舍五入保留两位小数。

数据范围

对于 10 \% 的数据，n \leq 1；

对于 30 \% 的数据，n \leq 2；

对于 60 \% 的数据，n \leq 20；

对于 100 \% 的数据，1 \leq n \leq 500，0.3 < \mathrm{alpha} < \frac{\pi}{2}，0 < h_i \leq 100，0 < r_i \leq 100。

by registerGen @ 2020-02-16 16:41:51

类型：题面修改

题目：P3377 【模板】左偏树（可并堆）

题目描述

如题，一开始有 n 个小根堆，每个堆包含且仅包含一个数。接下来需要支持两种操作：

操作 1：1 x y 将第 x 个数和第 y 个数所在的小根堆合并（若第 x 或第 y 个数已经被删除或第 x 和第 y 个数在用一个堆内，则无视此操作）。

操作 2：2 x 输出第 x 个数所在的堆最小数，并将其删除（若第 x 个数已经被删除，则输出 -1 并无视删除操作）。

输入格式

第一行包含两个正整数 n、m，分别表示一开始小根堆的个数和接下来操作的个数。

第二行包含 n 个正整数，其中第 i 个正整数表示第 i 个小根堆初始时包含且仅包含的数。

接下来 m 行每行 2 个或 3 个正整数，表示一条操作，格式如下：

操作 1：1 x y

操作 2：2 x

输出格式

输出包含若干行整数，分别依次对应每一个操作 2 所得的结果。

说明/提示

当堆里有多个最小值时，优先删除原序列的靠前的，否则会影响后续操作 1 导致 WA。

时空限制：1000 ms，128 M

【数据规模】

对于 30\% 的数据：n\le 10，m\le 10

对于 70\% 的数据：n\le 10^3，m\le 10^3

对于 100\% 的数据：n\le 10^5，m\le 10^5

【样例说明】

初始状态下，五个小根堆分别为：\{1\}、\{5\}、\{4\}、\{2\}、\{3\}。

第一次操作，将第 1 个数所在的小根堆与第 5 个数所在的小根堆合并，故变为四个小根堆：\{1,3\}、\{5\}、\{4\}、\{2\}。

第二次操作，将第 2 个数所在的小根堆与第 5 个数所在的小根堆合并，故变为三个小根堆：\{1,3,5\}、\{4\}、\{2\}。

第三次操作，将第 2 个数所在的小根堆的最小值输出并删除，故输出 1，第一个数被删除，三个小根堆为：\{3,5\}、\{4\}、\{2\}。

第四次操作，将第 4 个数所在的小根堆与第 2 个数所在的小根堆合并，故变为两个小根堆：\{2,3,5\}、\{4\}。

第五次操作，将第 2 个数所在的小根堆的最小值输出并删除，故输出 2，第四个数被删除，两个小根堆为：\{3,5\}、\{4\}。

故输出依次为 1、2。

## 题目描述
如题，一开始有 $n$ 个小根堆，每个堆包含且仅包含一个数。接下来需要支持两种操作：

操作 $1$：$1$ $x$ $y$ 将第 $x$ 个数和第 $y$ 个数所在的小根堆合并（若第 $x$ 或第 $y$ 个数已经被删除或第 $x$ 和第 $y$ 个数在用一个堆内，则无视此操作）。

操作 $2$：$2$ $x$ 输出第 $x$ 个数所在的堆最小数，并将其删除（若第 $x$ 个数已经被删除，则输出 $-1$ 并无视删除操作）。

## 输入格式
第一行包含两个正整数 $n$、$m$，分别表示一开始小根堆的个数和接下来操作的个数。

第二行包含 $n$ 个正整数，其中第 $i$ 个正整数表示第 $i$ 个小根堆初始时包含且仅包含的数。

接下来 $m$ 行每行 $2$ 个或 $3$ 个正整数，表示一条操作，格式如下：

操作 $1$：$1$ $x$ $y$

操作 $2$：$2$ $x$

## 输出格式
输出包含若干行整数，分别依次对应每一个操作 $2$ 所得的结果。

## 说明/提示
当堆里有多个最小值时，优先删除原序列的靠前的，否则会影响后续操作 $1$ 导致 WA。

时空限制：$1000$ ms，$128$ M

【数据规模】

对于 $30\%$ 的数据：$n\le 10$，$m\le 10$

对于 $70\%$ 的数据：$n\le 10^3$，$m\le 10^3$

对于 $100\%$ 的数据：$n\le 10^5$，$m\le 10^5$

【样例说明】

初始状态下，五个小根堆分别为：$\{1\}$、$\{5\}$、$\{4\}$、$\{2\}$、$\{3\}$。

第一次操作，将第 $1$ 个数所在的小根堆与第 $5$ 个数所在的小根堆合并，故变为四个小根堆：$\{1,3\}$、$\{5\}$、$\{4\}$、$\{2\}$。

第二次操作，将第 $2$ 个数所在的小根堆与第 $5$ 个数所在的小根堆合并，故变为三个小根堆：$\{1,3,5\}$、$\{4\}$、$\{2\}$。

第三次操作，将第 $2$ 个数所在的小根堆的最小值输出并删除，故输出 $1$，第一个数被删除，三个小根堆为：$\{3,5\}$、$\{4\}$、$\{2\}$。

第四次操作，将第 $4$ 个数所在的小根堆与第 $2$ 个数所在的小根堆合并，故变为两个小根堆：$\{2,3,5\}$、$\{4\}$。

第五次操作，将第 $2$ 个数所在的小根堆的最小值输出并删除，故输出 $2$，第四个数被删除，两个小根堆为：$\{3,5\}$、$\{4\}$。

故输出依次为 $1$、$2$。

@StudyingFather

by 81179332_ @ 2020-02-16 17:07:43

类型：题目修改

题目：P3345 [ZJOI2015]幻想乡战略游戏

### 题目描述

傲娇少女幽香正在玩一个非常有趣的战略类游戏，本来这个游戏的地图其实还不算太大，幽香还能管得过来，但是不知道为什么现在的网游厂商把游戏的地图越做越大，以至于幽香一眼根本看不过来，更别说和别人打仗了。

在打仗之前，幽香现在面临一个非常基本的管理问题需要解决。 整个地图是一个树结构，一共有 $n$ 块空地，这些空地被 $n-1$ 条带权边连接起来，使得每两个点之间有一条唯一的路径将它们连接起来。

在游戏中，幽香可能在空地上增加或者减少一些军队。同时，幽香可以在一个空地上放置一个补给站。 如果补给站在点 $u$ 上，并且空地 $v$ 上有$d_v$个单位的军队，那么幽香每天就要花费 $d_v \times dist(u,v)$ 的金钱来补给这些军队。

由于幽香需要补给所有的军队，因此幽香总共就要花费为 $\sum d_v \times dist$ ,其中 $1\le V\le n$ )的代价。其中 $dist(u,v)$ 表示 $u$ 与 $v$ 在树上的距离（唯一路径的权和）。

因为游戏的规定，幽香只能选择一个空地作为补给站。在游戏的过程中，幽香可能会在某些空地上制造一些军队，也可能会减少某些空地上的军队，进行了这样的操作以后，出于经济上的考虑，幽香往往可以移动他的补给站从而省一些钱。

但是由于这个游戏的地图是在太大了，幽香无法轻易的进行最优的安排，你能帮帮她吗？ 你可以假定一开始所有空地上都没有军队。

### 输入格式
第一行两个数 $n$ 和 $Q$ 分别表示树的点数和幽香操作的个数，其中点从 $1$ 到 $n$ 标号。

接下来 $n-1$ 行，每行三个正整数 $a,b,c$，表示 $a$ 和 $b$ 之间有一条边权为 $c$ 的边。

接下来 $Q$ 行，每行两个数 $u,e$，表示幽香在点 $u$ 上放了 $e$ 单位个军队（如果 $e<0$，就相当于是幽香在 $u$ 上减少了 $|e|$ 单位个军队，说白了就是 $d_u←d_u+e$ ）。

数据保证任何时刻每个点上的军队数量都是非负的。

### 输出格式
对于幽香的每个操作，输出操作完成以后，每天的最小花费，也即如果幽香选择最优的补给点进行补给时的花费。

### 说明/提示
对于所有数据，$1\le c\le 1000,0\le|e|\le1000, n\le10^5, Q\le10^5$ 

非常神奇的是，对于所有数据，这棵树上的点的度数都不超过 $20$，且$n,Q\ge 1$

by Limit @ 2020-02-17 10:49:31

类型: 模板题提供

题目: 【模板】区间修改可持久化线段树

题目: 【模板】区间修改可持久化线段树升级版

by NaCly_Fish @ 2020-02-17 11:58:34

@Sxy_Limit 话说对于区间修改主席树，P5055 是不是算已经包括在内了