[AGC006E] Rotate 3x3

我们有一个 $3$ 行 $N$ 列的初始矩阵，$(i,j)$ 位置的数为 $i+3j-3$。 我们有一个这样的操作：选择一个 $3 \times 3$ 的子矩阵，将这个子矩阵旋转 $180°$（具体见下面的图）。 现在给出一个 $3$ 行 $N$ 列的矩阵（矩阵中的数各不相同），问能否通过若干次上述操作将初始矩阵变为给定的矩阵。 翻译提供者：WAAutoMaton

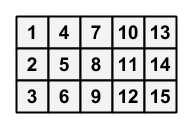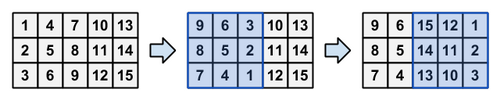[problemUrl]: https://atcoder.jp/contests/agc006/tasks/agc006_e 縦 $ 3 $ マス、横 $ N $ マスのマス目があります。 上から $ i $ マス目、左から $ j $ マス目のマスを ($ i $, $ j $) と表します。 最初、マス ($ i $, $ j $) には整数 $ i+3j-3 $ が書かれています。 $ N=5 $ のマス目 すぬけ君は次の操作を何回か行うことができます。 - $ 3×3 $ マスの正方形を選び、正方形内の整数の配置を $ 180° $ 回転する。 操作列の例（青い正方形が操作を行った部分） すぬけ君の目標は、マス ($ i $, $ j $) に整数 $ a_{i,j} $ が書かれているようにすることです。 すぬけ君が目標を達成できるか判定してください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ a_{1,1} $ $ a_{1,2} $ $ ... $ $ a_{1,N} $ $ a_{2,1} $ $ a_{2,2} $ $ ... $ $ a_{2,N} $ $ a_{3,1} $ $ a_{3,2} $ $ ... $ $ a_{3,N} $

すぬけ君が目標を達成できるならば `Yes` を、できないならば `No` を出力せよ。

5
9 6 15 12 1
8 5 14 11 2
7 4 13 10 3

Yes

5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15

No

5
1 4 7 10 13
2 5 8 11 14
3 6 9 12 15

Yes

6
15 10 3 4 9 16
14 11 2 5 8 17
13 12 1 6 7 18

Yes

7
21 12 1 16 13 6 7
20 11 2 17 14 5 8
19 10 3 18 15 4 9

No

### 制約 - $ 5\ <\ =N\ <\ =10^5 $ - $ 1\ <\ =a_{i,j}\ <\ =3N $ - $ a_{i,j} $ はすべて相異なる。 ### Sample Explanation 1 問題文中の図の例です。 ### Sample Explanation 3 最初から目標の配置になっています。