AT_abc358_f [ABC358F] Easiest Maze

[problemUrl]: https://atcoder.jp/contests/abc358/tasks/abc358_f すぬけくんは、AtCoder Land の新たな目玉アトラクションとして迷路を建設しようと考えています。 迷路は縦 $ N $ 行・横 $ M $ 列のグリッドとして表され、右上のマスの上端が入口、右下のマスの下端が出口です。 すぬけくんは、隣接するマスの間に適切に壁を配置することで迷路を作ります。 すぬけくんは簡単な迷路が大好きなので、入口から出口までの道順は枝分かれを一切持たずにちょうど $ K $ マスを通るようなものにしたいです。 そのような迷路を作ることが可能か判定し、可能ならば $ 1 $ つ構築してください。 例えば以下の図では、$ N=3,M=3 $ であり、実線で書かれているところに壁が配置されています（入口と出口を除く外周部には必ず壁が配置されるものとします）。 このとき、入口から出口までの道順は枝分かれを一切持たずにちょうど $ 7 $ マスを通っています。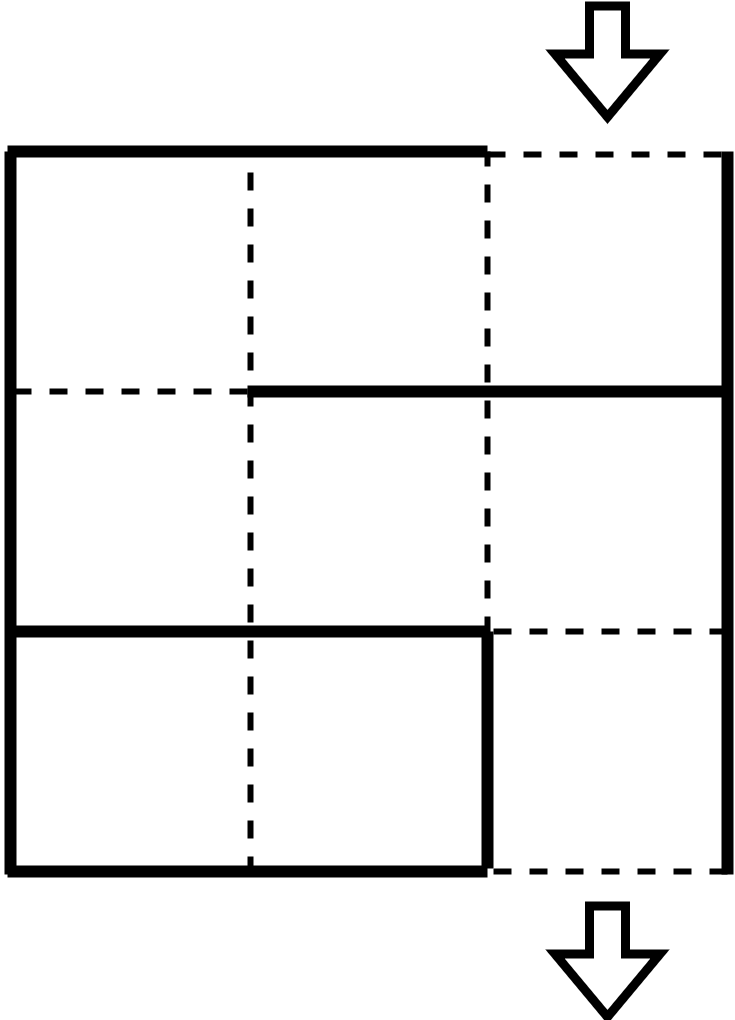  厳密には以下の通りです。 縦 $ N $ 行・横 $ M $ 列のグリッドがあります。 上から $ i $ 行目、左から $ j $ 列目のマスを $ (i,j) $ と表記します。 あなたは、辺で隣接する任意の $ 2 $ マスの間それぞれについて壁を置くか置かないか決めることができます。 壁を置く場所をうまく定めることで以下の条件を満たすことができるか判定し、できるならば実際に $ 1 $ つ構築してください。 > $ NM $ 頂点からなる無向グラフ $ G $ を考える。$ G $ の各頂点は $ 2 $ つの整数の組 $ (i,j)\ (1\leq\ i\leq\ N,\ 1\leq\ j\leq\ M) $ によって互いに相異なるラベルが付けられている。 相異なる $ 2 $ 頂点 $ (i_1,j_1),(i_2,j_2) $ は、$ |i_1-i_2|+|j_1-j_2|=1 $ かつグリッド上の $ 2 $ マス $ (i_1,j_1),(i_2,j_2) $ の間に壁が置かれていない場合、またその場合に限り辺で結ばれている。 > > 条件：$ K $ 頂点からなり $ 2 $ 頂点 $ (1,M),(N,M) $ を結ぶような単純パスが存在し、また $ 2 $ 頂点 $ (1,M),(N,M) $ を含む連結成分はこのパスのみからなる。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ K $

条件を満たす壁の配置が存在しないならば `No` を出力し、存在するならばそのうちの $ 1 $ つを以下の形式で出力せよ。 条件を満たす壁の配置が複数存在する場合は、そのどれを出力してもよい。 **複雑な出力形式のため、下記の出力例も参考にしてください。** > Yes +++++ $ \dots $ +++S+ +o?o? $ \dots $ ?o?o+ +?+?+ $ \dots $ +?+?+ +o?o? $ \dots $ ?o?o+ +?+?+ $ \dots $ +?+?+ $ \vdots $ +o?o? $ \dots $ ?o?o+ +?+?+ $ \dots $ +?+?+ +o?o? $ \dots $ ?o?o+ +++++ $ \dots $ +++G+ ここで、`S`, `G`, `+`, `o` はそれぞれ入口、出口、壁、マスを表し、マスとマスの間にある `?` は壁を置くことができる場所である。 横に隣接する $ 2 $ マスの間にある `?` は、壁を置くならば `|` で、壁を置かないならば `.` で置き換えよ。 縦に隣接する $ 2 $ マスの間にある `?` は、壁を置くならば `-` で、壁を置かないならば `.` で置き換えよ。 厳密には以下の通りである。 - 出力は $ 2N+2 $ 行からなり、$ 1 $ 行目には文字列 `Yes` を、$ 2 $ 行目から $ 2N+2 $ 行目には以下で説明されるように長さ $ 2M+1 $ の文字列を出力する。 - $ 2 $ 行目には、$ 2M-1 $ 個の `+`, `S`, `+` をこの順に連結して出力する。 - $ 1+2i $ 行目 $ (1\leq\ i\leq\ N) $ には、`+`, `o`, $ c_{i,1} $, `o`, $ c_{i,2} $, $ \dots $, $ c_{i,M-1} $, `o`, `+` をこの順に連結して出力する。 ここで、$ c_{i,j} $ はマス $ (i,j),(i,j+1) $ の間に壁を置くならば `|`、置かないならば `.` である。 - $ 2+2i $ 行目 $ (1\leq\ i\leq\ N-1) $ には、`+`, $ r_{i,1} $, `+`, $ r_{i,2} $, `+`, $ \dots $, `+`, $ r_{i,M} $, `+` をこの順に連結して出力する。 ここで、$ r_{i,j} $ はマス $ (i,j),(i+1,j) $ の間に壁を置くならば `-`、置かないならば `.` である。 - $ 2N+2 $ 行目には、$ 2M-1 $ 個の `+`, `G`, `+` をこの順に連結して出力する。

### 制約 - $ 2\leq\ N\ \leq\ 100 $ - $ 1\leq\ M\ \leq\ 100 $ - $ 1\leq\ K\leq\ NM $ - 入力は全て整数 ### Sample Explanation 1 問題文中の図と同じ壁の配置です。