[AGC039E] Pairing Points

在一个圆上有 $2 N$ 个点，其中有一些点对之间有连线，给出了连线的邻接矩阵 $A_{i, j}$。 并且保证不存在三线共点的情况。 你需要选择其中 $N$ 条线保留下来，使得每个点恰好连一条线，并且这 $N$ 条线画出来后构成一棵树。  如图，左上角是合法的情况，右上角连出环了，左下角不是连通的，右下角不符合每个点恰好连一条线。 请求出不同的连线方案的数量。 - $1 \le N \le 20$。

[problemUrl]: https://atcoder.jp/contests/agc039/tasks/agc039_e 円周上の一般の位置に相異なる $ 2N $ 個の点が並んでおり、反時計回りに順に $ 1,\dots,2N $ の番号が付けられています。 ただし、ここでいう一般の位置とは、どの相異なる $ 6 $ 点 $ U,\ V,\ W,\ X,\ Y,\ Z $ についても、線分 $ UV,\ WX,\ YZ $ が一点で交わらないことをいいます。 また、 $ 2N\ \times\ 2N $ の行列 $ A $ が与えられます。 円周上の $ 2N $ 個の点を $ N $ 個のペアに分ける方法であって、以下の条件をみたすようなものの個数を求めてください。 - すべてのペアに対してそのペアの $ 2 $ つの点を結ぶ赤い線分をひいたとき、赤い部分が "木" になっている。 - すべてのペアについて、その端点を点 $ P,\ Q $ としたとき、 $ A_{P,Q}\ =\ A_{Q,P}\ =\ 1 $ である。 より厳密には、赤い部分が "木" になっているとは、赤い部分全体が連結かつ無閉路になっていることを指します。 例えば、下図において、 - 左上の例は条件を満たします。 - 右上の例は、赤い部分に閉路が存在し、条件を満たしません。 - 左下の例は、赤い部分が非連結であり、条件を満たしません。 - 右下の例は、ペアに属さない頂点やペアに複数回含まれる頂点が存在し、条件を満たしません。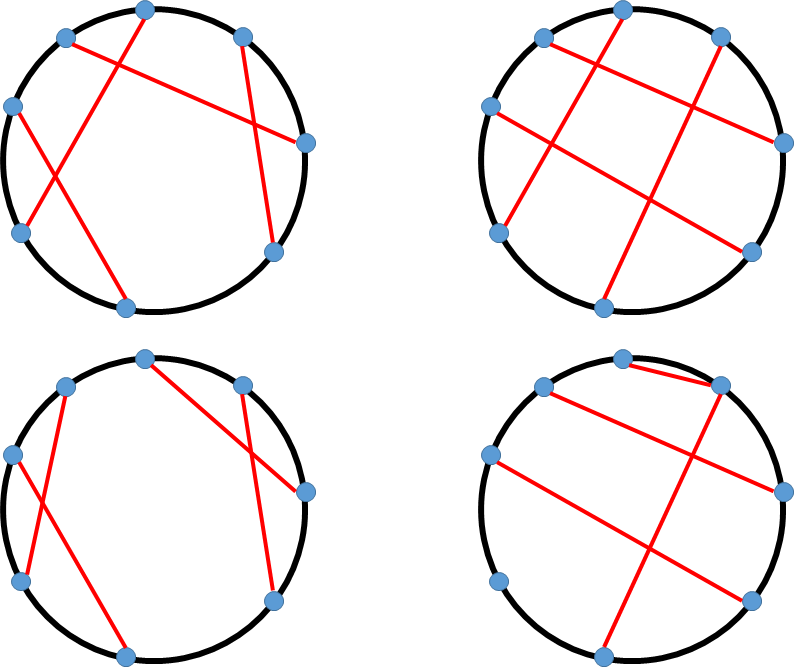 図: 条件を満たす例 (左上) とそうでない例 (それ以外)

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A_{1,1}...A_{1,2N} $ $ : $ $ A_{2N,1}...A_{2N,2N} $

円周上の $ 2N $ 個の点を $ N $ 個のペアに分ける方法であって、条件をみたすようなものの個数を出力せよ。 この制約下で、答えが $ 64 $ ビット符号付整数の範囲内に収まることが証明できる。

3
011111
101111
110111
111011
111101
111110

3

4
01111100
10011111
10011100
11101111
11110111
11111011
01011101
01011110

6

8
0111101111111111
1011101111111111
1101101111011101
1110111111111111
1111011111110111
0001101111111111
1111110111011111
1111111011111111
1111111101111111
1111111110111111
1101110111011111
1111111111101111
1111011111110111
1111111111111011
1101111111111101
1111111111111110

4762

### ノート 答えは、$ 2N $ 個の点が一般の位置にある限り、その具体的な位置関係には依存しないことが証明できます。 ### 制約 - $ 1\ \leq\ N\ \leq\ 20 $ - $ A_{i,j} $ は `0` または `1` である - $ A_{i,i} $ は `0` である - $ A_{i,j}=A_{j,i} $ - $ N $ は整数である ### Sample Explanation 1 $ ((1,4),(2,6),(3,5)) $, $ ((1,3),(2,5),(4,6)) $, $ ((1,5),(2,4),(3,6)) $ の $ 3 $ つの分け方が条件を満たします。