AT_codefestival_2016_final_g Zigzag MST
题目描述
有一个包含 $N$ 个顶点的图,顶点编号为 $0$ 到 $N-1$。初始时没有任何边。
你需要处理 $Q$ 个添加边的操作。对于第 $i$ 个操作($1 \leq i \leq Q$),会给出三个整数 $A_i,\ B_i,\ C_i$,然后按如下方式无限次地添加边:
- 添加一条连接 $A_i$ 号顶点和 $B_i$ 号顶点、权值为 $C_i$ 的无向边。
- 添加一条连接 $B_i$ 号顶点和 $A_i+1$ 号顶点、权值为 $C_i+1$ 的无向边。
- 添加一条连接 $A_i+1$ 号顶点和 $B_i+1$ 号顶点、权值为 $C_i+2$ 的无向边。
- 添加一条连接 $B_i+1$ 号顶点和 $A_i+2$ 号顶点、权值为 $C_i+3$ 的无向边。
- 添加一条连接 $A_i+2$ 号顶点和 $B_i+2$ 号顶点、权值为 $C_i+4$ 的无向边。
- 添加一条连接 $B_i+2$ 号顶点和 $A_i+3$ 号顶点、权值为 $C_i+5$ 的无向边。
- 添加一条连接 $A_i+3$ 号顶点和 $B_i+3$ 号顶点、权值为 $C_i+6$ 的无向边。
- 以此类推……
其中,顶点编号均按 $N$ 取模。例如,$N$ 号顶点等同于 $0$ 号顶点,$2N-1$ 号顶点等同于 $N-1$ 号顶点。
例如,当 $N=16,\ A_i=7,\ B_i=14,\ C_i=1$ 时,添加的前 $7$ 条边如下图所示:
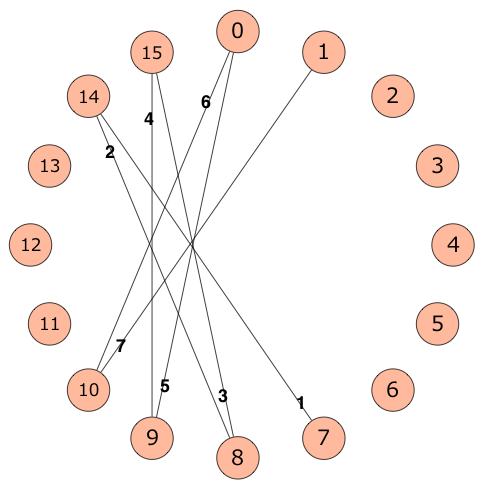
请你求出,所有边都添加完毕后,该图的最小生成树中所有边的权值之和。
输入格式
输入以如下格式从标准输入读入:
> $N$ $Q$ $A_1$ $B_1$ $C_1$ $A_2$ $B_2$ $C_2$ : $A_Q$ $B_Q$ $C_Q$
输出格式
输出最小生成树中所有边的权值之和。
说明/提示
## 限制
- $2 \leq N \leq 200,\!000$
- $1 \leq Q \leq 200,\!000$
- $0 \leq A_i,B_i \leq N-1$
- $1 \leq C_i \leq 10^9$
## 样例解释 1
最小生成树如下图所示。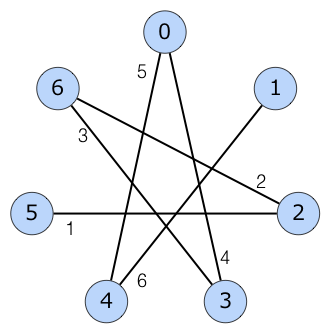
注意,图中可能存在重边。
## 样例解释 2
注意,图中可能存在自环。
由 ChatGPT 4.1 翻译