CF1019C Sergey's problem
Description
Sergey just turned five years old! When he was one year old, his parents gave him a number; when he was two years old, his parents gave him an array of integers. On his third birthday he received a string. When he was four, his mother woke him up in a quiet voice, wished him to be a good boy and gave him a rooted tree. Today he celebrates his birthday again! He found a directed graph without loops as a present from his parents.
Since Sergey is a very curious boy, he immediately came up with a thing to do. He decided to find a set $ Q $ of vertices in this graph, such that no two vertices $ x, y \in Q $ are connected by an edge, and it is possible to reach any vertex $ z \notin Q $ from some vertex of $ Q $ in no more than two moves.
After a little thought, Sergey was able to solve this task. Can you solve it too?
A vertex $ y $ is reachable from a vertex $ x $ in at most two moves if either there is a directed edge $ (x,y) $ , or there exist two directed edges $ (x,z) $ and $ (z, y) $ for some vertex $ z $ .
Input Format
N/A
Output Format
N/A
Explanation/Hint
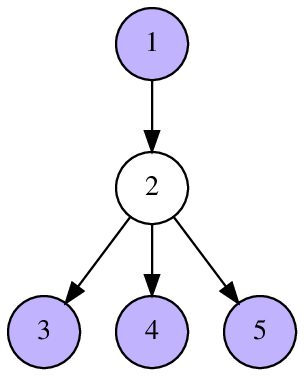
In the first sample, the vertices $ 1, 3, 4, 5 $ are not connected. The vertex $ 2 $ is reachable from vertex $ 1 $ by one edge.
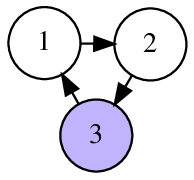
In the second sample, it is possible to reach the vertex $ 1 $ in one move and the vertex $ 2 $ in two moves.
The following pictures illustrate sample tests and their answers.