CF10B Cinema Cashier

All cinema halls in Berland are rectangles with $ K $ rows of $ K $ seats each, and $ K $ is an odd number. Rows and seats are numbered from $ 1 $ to $ K $ . For safety reasons people, who come to the box office to buy tickets, are not allowed to choose seats themselves. Formerly the choice was made by a cashier, but now this is the responsibility of a special seating program. It was found out that the large majority of Berland's inhabitants go to the cinema in order to watch a movie, that's why they want to sit as close to the hall center as possible. Moreover, a company of $ M $ people, who come to watch a movie, want necessarily to occupy $ M $ successive seats in one row. Let's formulate the algorithm, according to which the program chooses seats and sells tickets. As the request for $ M $ seats comes, the program should determine the row number $ x $ and the segment $ [y_{l},y_{r}] $ of the seats numbers in this row, where $ y_{r}-y_{l}+1=M $ . From all such possible variants as a final result the program should choose the one with the minimum function value of total seats remoteness from the center. Say, 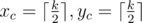 — the row and the seat numbers of the most "central" seat. Then the function value of seats remoteness from the hall center is 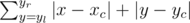. If the amount of minimum function values is more than one, the program should choose the one that is closer to the screen (i.e. the row number $ x $ is lower). If the variants are still multiple, it should choose the one with the minimum $ y_{l} $ . If you did not get yet, your task is to simulate the work of this program.

N/A

N/A