CF1110G Tree-Tac-Toe

给出一棵 $N$ 个点的树，初始时某些节点是白色，其他节点没有颜色。 有两个人在树上博弈。每一回合，一方可以将一个没有颜色的点染成白色，然后另一方可以将一个没有颜色的点染成黑色。白色方为先手，黑色方为后手。 如果在某次染色后树上存在三个点 $ABC$ 满足有边 $(A,B)(B,C)$、$ABC$ 都有颜色且颜色相同，则该颜色对应的人获胜。 假设两人绝顶聪明，问最后结果如何。

无

无

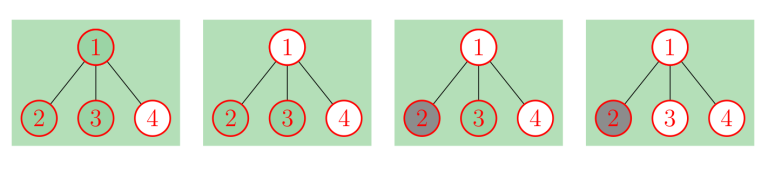In the first example, vertex $ 4 $ is already colored in white. The white player can win by coloring the vertex $ 1 $ in white first and the remaining vertex on his second turn. The process is illustrated with the pictures below. In the second example, we can show that no player can enforce their victory.