CF1110G Tree-Tac-Toe

The tic-tac-toe game is starting on a tree of $ n $ vertices. Some vertices are already colored in white while the remaining are uncolored. There are two players — white and black. The players make moves alternatively. The white player starts the game. In his turn, a player must select one uncolored vertex and paint it in his color. The player wins if he paints some path of three vertices in his color. In case all vertices are colored and neither player won, the game ends in a draw. Could you please find who will win the game or whether it ends as a draw, assuming both players play optimally?

N/A

N/A

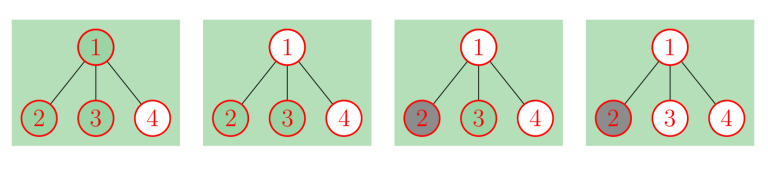In the first example, vertex $ 4 $ is already colored in white. The white player can win by coloring the vertex $ 1 $ in white first and the remaining vertex on his second turn. The process is illustrated with the pictures below. In the second example, we can show that no player can enforce their victory.