CF1190D Tokitsukaze and Strange Rectangle

There are $ n $ points on the plane, the $ i $ -th of which is at $ (x_i, y_i) $ . Tokitsukaze wants to draw a strange rectangular area and pick all the points in the area. The strange area is enclosed by three lines, $ x = l $ , $ y = a $ and $ x = r $ , as its left side, its bottom side and its right side respectively, where $ l $ , $ r $ and $ a $ can be any real numbers satisfying that $ l < r $ . The upper side of the area is boundless, which you can regard as a line parallel to the $ x $ -axis at infinity. The following figure shows a strange rectangular area. 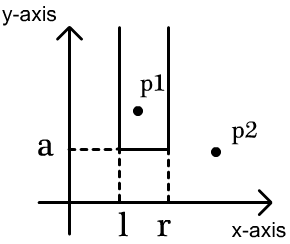A point $ (x_i, y_i) $ is in the strange rectangular area if and only if $ l < x_i < r $ and $ y_i > a $ . For example, in the above figure, $ p_1 $ is in the area while $ p_2 $ is not. Tokitsukaze wants to know how many different non-empty sets she can obtain by picking all the points in a strange rectangular area, where we think two sets are different if there exists at least one point in one set of them but not in the other.

N/A

N/A

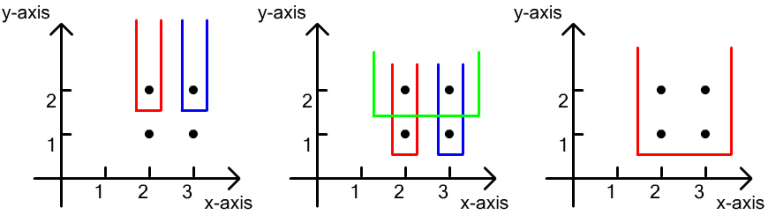
For the first example, there is exactly one set having $ k $ points for $ k = 1, 2, 3 $ , so the total number is $ 3 $ . For the second example, the numbers of sets having $ k $ points for $ k = 1, 2, 3 $ are $ 3 $ , $ 2 $ , $ 1 $ respectively, and their sum is $ 6 $ . For the third example, as the following figure shows, there are - $ 2 $ sets having one point; - $ 3 $ sets having two points; - $ 1 $ set having four points. Therefore, the number of different non-empty sets in this example is $ 2 + 3 + 0 + 1 = 6 $ .