Count The Rectangles
题意翻译
二维坐标系上有 $n$ 条线段，每条线段连接 $(x_{i,1},y_{i,1}),(x_{i,2},y_{i,2})$ 两个整点，且所有线段平行于坐标轴，保证平行于同一条坐标轴的线段不相交。求这些线段能组成多少个矩形。
$(1 \leq n \leq 5 \times 10^3,x,y \in [-5 \times 10^3,5 \times 10^3])$
题目描述
There are $ n $ segments drawn on a plane; the $ i $ -th segment connects two points ( $ x_{i, 1} $ , $ y_{i, 1} $ ) and ( $ x_{i, 2} $ , $ y_{i, 2} $ ). Each segment is non-degenerate, and is either horizontal or vertical — formally, for every $ i \in [1, n] $ either $ x_{i, 1} = x_{i, 2} $ or $ y_{i, 1} = y_{i, 2} $ (but only one of these conditions holds). Only segments of different types may intersect: no pair of horizontal segments shares any common points, and no pair of vertical segments shares any common points.
We say that four segments having indices $ h_1 $ , $ h_2 $ , $ v_1 $ and $ v_2 $ such that $ h_1 < h_2 $ and $ v_1 < v_2 $ form a rectangle if the following conditions hold:
- segments $ h_1 $ and $ h_2 $ are horizontal;
- segments $ v_1 $ and $ v_2 $ are vertical;
- segment $ h_1 $ intersects with segment $ v_1 $ ;
- segment $ h_2 $ intersects with segment $ v_1 $ ;
- segment $ h_1 $ intersects with segment $ v_2 $ ;
- segment $ h_2 $ intersects with segment $ v_2 $ .
Please calculate the number of ways to choose four segments so they form a rectangle. Note that the conditions $ h_1 < h_2 $ and $ v_1 < v_2 $ should hold.
输入输出格式
输入格式
The first line contains one integer $ n $ ( $ 1 \le n \le 5000 $ ) — the number of segments.
Then $ n $ lines follow. The $ i $ -th line contains four integers $ x_{i, 1} $ , $ y_{i, 1} $ , $ x_{i, 2} $ and $ y_{i, 2} $ denoting the endpoints of the $ i $ -th segment. All coordinates of the endpoints are in the range $ [-5000, 5000] $ .
It is guaranteed that each segment is non-degenerate and is either horizontal or vertical. Furthermore, if two segments share a common point, one of these segments is horizontal, and another one is vertical.
输出格式
Print one integer — the number of ways to choose four segments so they form a rectangle.
输入输出样例
输入样例 #1
7
-1 4 -1 -2
6 -1 -2 -1
-2 3 6 3
2 -2 2 4
4 -1 4 3
5 3 5 1
5 2 1 2
输出样例 #1
7
输入样例 #2
5
1 5 1 0
0 1 5 1
5 4 0 4
4 2 4 0
4 3 4 5
输出样例 #2
0
说明
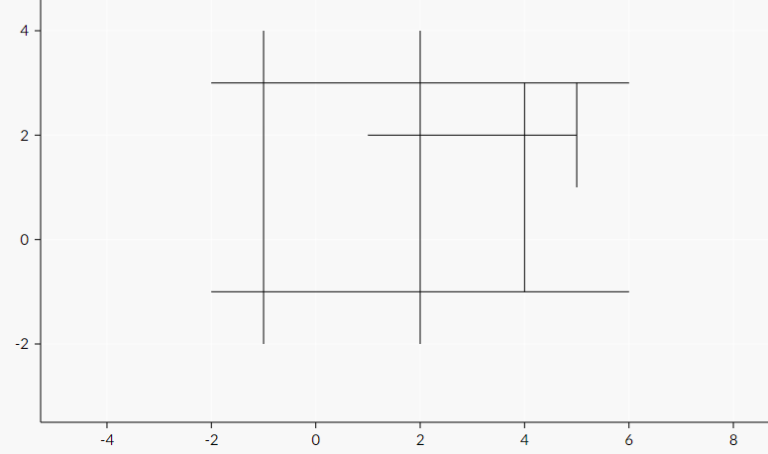
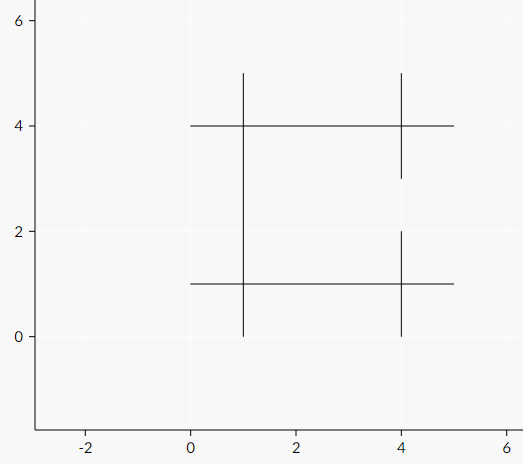
The following pictures represent sample cases:
 