Graph Traveler

Gildong正在试验一个有趣的Graph Traveler,具体来说,这个Graph Traveler是个由n个编号为1-n的点构成的有向图,第i个点有$m_i$条出边,边到达的点分别被记为$e_i[0],e_i[1]...e_i[m_i-1]$.每个点还有点权$k_i$ 现在有$q$个询问,每个询问要求从某个点开始,初始有个点权$c$,每次到一个点$i$(起点也算)就把点权$c$加上$k_i$,然后走$i$的出边$e_i[x](x \equiv c\mod m_i)$.可以发现这个过程是会一直进行下去的.现在问每次这样走,图上有多少个点会被经过无限次

Gildong is experimenting with an interesting machine Graph Traveler. In Graph Traveler, there is a directed graph consisting of $ n $ vertices numbered from $ 1 $ to $ n $ . The $ i $ -th vertex has $ m_i $ outgoing edges that are labeled as $ e_i[0] $ , $ e_i[1] $ , $ \ldots $ , $ e_i[m_i-1] $ , each representing the destination vertex of the edge. The graph can have multiple edges and self-loops. The $ i $ -th vertex also has an integer $ k_i $ written on itself. A travel on this graph works as follows. 1. Gildong chooses a vertex to start from, and an integer to start with. Set the variable $ c $ to this integer. 2. After arriving at the vertex $ i $ , or when Gildong begins the travel at some vertex $ i $ , add $ k_i $ to $ c $ . 3. The next vertex is $ e_i[x] $ where $ x $ is an integer $ 0 \le x \le m_i-1 $ satisfying $ x \equiv c \pmod {m_i} $ . Go to the next vertex and go back to step 2. It's obvious that a travel never ends, since the 2nd and the 3rd step will be repeated endlessly. For example, assume that Gildong starts at vertex $ 1 $ with $ c = 5 $ , and $ m_1 = 2 $ , $ e_1[0] = 1 $ , $ e_1[1] = 2 $ , $ k_1 = -3 $ . Right after he starts at vertex $ 1 $ , $ c $ becomes $ 2 $ . Since the only integer $ x $ ( $ 0 \le x \le 1 $ ) where $ x \equiv c \pmod {m_i} $ is $ 0 $ , Gildong goes to vertex $ e_1[0] = 1 $ . After arriving at vertex $ 1 $ again, $ c $ becomes $ -1 $ . The only integer $ x $ satisfying the conditions is $ 1 $ , so he goes to vertex $ e_1[1] = 2 $ , and so on. Since Gildong is quite inquisitive, he's going to ask you $ q $ queries. He wants to know how many distinct vertices will be visited infinitely many times, if he starts the travel from a certain vertex with a certain value of $ c $ . Note that you should not count the vertices that will be visited only finite times.

The first line of the input contains an integer $ n $ ( $ 1 \le n \le 1000 $ ), the number of vertices in the graph. The second line contains $ n $ integers. The $ i $ -th integer is $ k_i $ ( $ -10^9 \le k_i \le 10^9 $ ), the integer written on the $ i $ -th vertex. Next $ 2 \cdot n $ lines describe the edges of each vertex. The $ (2 \cdot i + 1) $ -st line contains an integer $ m_i $ ( $ 1 \le m_i \le 10 $ ), the number of outgoing edges of the $ i $ -th vertex. The $ (2 \cdot i + 2) $ -nd line contains $ m_i $ integers $ e_i[0] $ , $ e_i[1] $ , $ \ldots $ , $ e_i[m_i-1] $ , each having an integer value between $ 1 $ and $ n $ , inclusive. Next line contains an integer $ q $ ( $ 1 \le q \le 10^5 $ ), the number of queries Gildong wants to ask. Next $ q $ lines contains two integers $ x $ and $ y $ ( $ 1 \le x \le n $ , $ -10^9 \le y \le 10^9 $ ) each, which mean that the start vertex is $ x $ and the starting value of $ c $ is $ y $ .

For each query, print the number of distinct vertices that will be visited infinitely many times, if Gildong starts at vertex $ x $ with starting integer $ y $ .

4
0 0 0 0
2
2 3
1
2
3
2 4 1
4
3 1 2 1
6
1 0
2 0
3 -1
4 -2
1 1
1 5

1
1
2
1
3
2

4
4 -5 -3 -1
2
2 3
1
2
3
2 4 1
4
3 1 2 1
6
1 0
2 0
3 -1
4 -2
1 1
1 5

1
1
1
3
1
1

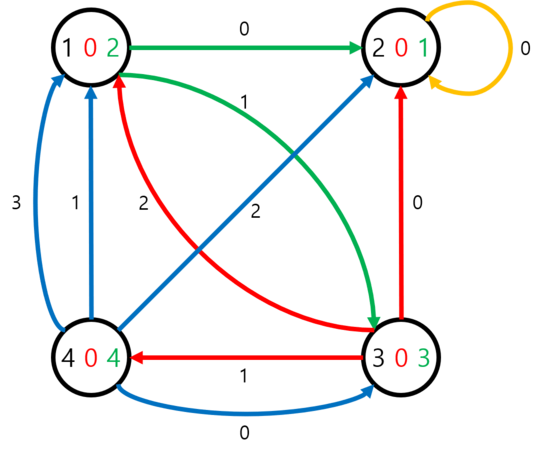The first example can be shown like the following image: Three integers are marked on $ i $ -th vertex: $ i $ , $ k_i $ , and $ m_i $ respectively. The outgoing edges are labeled with an integer representing the edge number of $ i $ -th vertex. The travel for each query works as follows. It is described as a sequence of phrases, each in the format "vertex ( $ c $ after $ k_i $ added)". - $ 1(0) \to 2(0) \to 2(0) \to \ldots $ - $ 2(0) \to 2(0) \to \ldots $ - $ 3(-1) \to 1(-1) \to 3(-1) \to \ldots $ - $ 4(-2) \to 2(-2) \to 2(-2) \to \ldots $ - $ 1(1) \to 3(1) \to 4(1) \to 1(1) \to \ldots $ - $ 1(5) \to 3(5) \to 1(5) \to \ldots $ The second example is same as the first example, except that the vertices have non-zero values. Therefore the answers to the queries also differ from the first example. 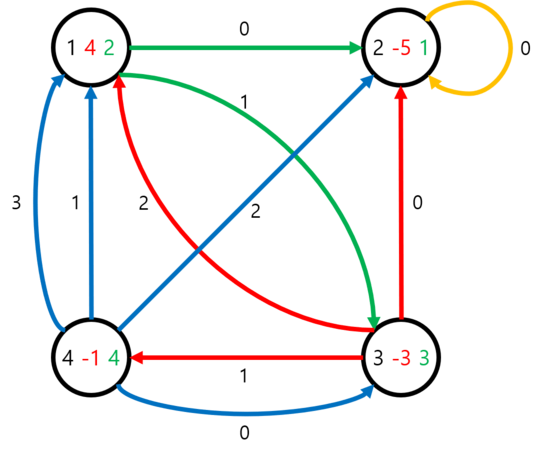The queries for the second example works as follows: - $ 1(4) \to 2(-1) \to 2(-6) \to \ldots $ - $ 2(-5) \to 2(-10) \to \ldots $ - $ 3(-4) \to 1(0) \to 2(-5) \to 2(-10) \to \ldots $ - $ 4(-3) \to 1(1) \to 3(-2) \to 4(-3) \to \ldots $ - $ 1(5) \to 3(2) \to 1(6) \to 2(1) \to 2(-4) \to \ldots $ - $ 1(9) \to 3(6) \to 2(1) \to 2(-4) \to \ldots $