CF1238F The Maximum Subtree

Assume that you have $ k $ one-dimensional segments $ s_1, s_2, \dots s_k $ (each segment is denoted by two integers — its endpoints). Then you can build the following graph on these segments. The graph consists of $ k $ vertexes, and there is an edge between the $ i $ -th and the $ j $ -th vertexes ( $ i \neq j $ ) if and only if the segments $ s_i $ and $ s_j $ intersect (there exists at least one point that belongs to both of them). 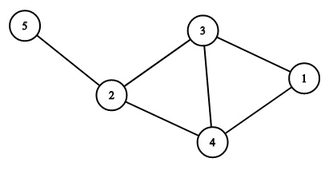For example, if $ s_1 = [1, 6], s_2 = [8, 20], s_3 = [4, 10], s_4 = [2, 13], s_5 = [17, 18] $ , then the resulting graph is the following: A tree of size $ m $ is good if it is possible to choose $ m $ one-dimensional segments so that the graph built on these segments coincides with this tree. You are given a tree, you have to find its good subtree with maximum possible size. Recall that a subtree is a connected subgraph of a tree. Note that you have to answer $ q $ independent queries.

N/A

N/A

In the first query there is a good subtree of size $ 8 $ . The vertices belonging to this subtree are $ {9, 4, 10, 2, 5, 1, 6, 3} $ .