CF1292C Xenon's Attack on the Gangs

在 A.R.C. Markland-N 的另一层楼，年轻人 Simon "Xenon" Jackson 在提前完成项目后（如往常一样）正在休息。由于有大量空闲时间，他决定发挥自己传奇黑客“X”的本能，去对抗网络世界中的黑帮。 他的目标是一个由 $n$ 个小黑帮组成的网络。该网络恰好有 $n-1$ 条直接连接，每条连接将两个黑帮连接在一起。这些连接的方式保证了任意两个黑帮之间都存在一条由直接连接组成的路径。 通过数据挖掘，Xenon 发现这些黑帮采用了一种交叉加密方式来防止被破获：每条连接被分配一个从 $0$ 到 $n-2$ 的整数，所有被分配的整数互不相同，并且每个整数都被分配给某条连接。如果有入侵者试图访问加密数据，他们需要突破 $S$ 层密码保护，其中 $S$ 的定义如下： $$ S = \sum_{1 \leq u < v \leq n} mex(u, v) $$ 其中，$mex(u, v)$ 表示在黑帮 $u$ 到黑帮 $v$ 的唯一简单路径上，没有出现的最小非负整数。 Xenon 并不知道这些整数的具体分配方式，但这对他来说不是问题。他决定让自己的 AI 实例尝试所有密码，但在此之前，他需要知道 $S$ 的最大可能值，以便高效部署 AI。 现在，Xenon 正在编写 AI 脚本，预计两小时后完成。在他回来之前，你能帮他求出 $S$ 的最大可能值吗？

第一行包含一个整数 $n$（$2 \leq n \leq 3000$），表示网络中的黑帮数量。 接下来的 $n-1$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1 \leq u_i, v_i \leq n$，$u_i \neq v_i$），表示黑帮 $u_i$ 和 $v_i$ 之间有一条直接连接。 保证这些连接的方式使得任意两个黑帮之间都恰好有一条简单路径。

输出一个整数，表示黑帮网络中密码层数 $S$ 的最大可能值。

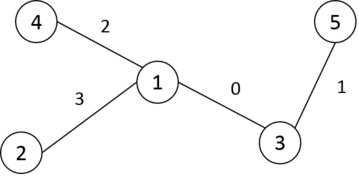
在第一个样例中，可以通过如下分配获得最大的 $S$：  在这种分配下，$mex(1, 2) = 0$，$mex(1, 3) = 2$，$mex(2, 3) = 1$。因此，$S = 0 + 2 + 1 = 3$。 在第二个样例中，可以通过如下分配获得最大的 $S$：  在这种分配下，所有非零的 $mex$ 值如下： - $mex(1, 3) = 1$ - $mex(1, 5) = 2$ - $mex(2, 3) = 1$ - $mex(2, 5) = 2$ - $mex(3, 4) = 1$ - $mex(4, 5) = 3$ 因此，$S = 1 + 2 + 1 + 2 + 1 + 3 = 10$。 由 ChatGPT 4.1 翻译