CF1304E 1-Trees and Queries
题目描述
Gildong 在登山时,走过了成千上万棵树。受到这些树的启发,他突然想到一个关于数据结构中树的有趣想法:如果我们在树中再添加一条边会怎样?
随后他发现,这样的类树图被称为 1-tree。由于 Gildong 已经厌倦了解决太多树的问题,他想看看在 1-tree 上是否也能用类似的技巧。不过,他并不打算自己解决,而是要通过给你关于 1-tree 的若干询问来考察你。
首先,他会给你一棵有 $n$ 个节点的树(不是 1-tree),然后他会问你 $q$ 个询问。每个询问包含 $5$ 个整数:$x$、$y$、$a$、$b$ 和 $k$。这意味着你需要判断,在给树的 $x$ 和 $y$ 节点之间添加一条双向边后,是否存在一条从 $a$ 到 $b$ 的路径,且该路径恰好经过 $k$ 条边。路径可以多次经过同一个节点和同一条边。所有询问彼此独立,即每次询问添加的边在下一个询问时会被移除。
输入格式
第一行包含一个整数 $n$($3 \le n \le 10^5$),表示树的节点数。
接下来的 $n-1$ 行,每行包含两个整数 $u$ 和 $v$($1 \le u,v \le n$,$u \ne v$),表示在节点 $u$ 和 $v$ 之间有一条边。所有边都是双向且互不相同。
接下来一行包含一个整数 $q$($1 \le q \le 10^5$),表示 Gildong 要问的询问数。
接下来的 $q$ 行,每行包含五个整数 $x$、$y$、$a$、$b$ 和 $k$($1 \le x,y,a,b \le n$,$x \ne y$,$1 \le k \le 10^9$),含义如题目描述所述。保证在原树中不存在 $x$ 和 $y$ 之间的边。
输出格式
对于每个询问,如果在添加 $x$ 和 $y$ 之间的边后,存在一条从 $a$ 到 $b$ 恰好经过 $k$ 条边的路径,则输出 "YES";否则输出 "NO"。
你可以用任意大小写输出每个字母。
说明/提示
下图描述了树(圆圈和实线)以及每个询问中添加的边(虚线)。
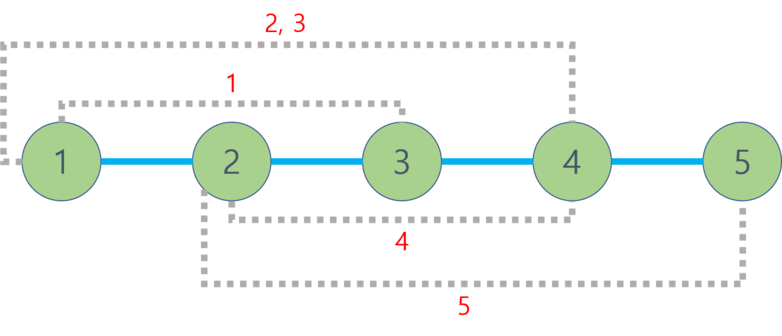
对于答案为 "YES" 的询问,可能的路径如下:
- 第 $1$ 个询问:$1$ – $3$ – $2$
- 第 $2$ 个询问:$1$ – $2$ – $3$
- 第 $4$ 个询问:$3$ – $4$ – $2$ – $3$ – $4$ – $2$ – $3$ – $4$ – $2$ – $3$
由 ChatGPT 4.1 翻译