CF1332E Height All the Same
题目描述
最近,Alice 迷上了一款名为 Sirtet 的游戏。
在 Sirtet 中,玩家会得到一个 $n \times m$ 的网格。初始时,格 $(i, j)$ 上码放有 $a_{i, j}$ 个方块。若两个格子有一条公共边,我们称这两个格子时相邻的。玩家可以进行以下两种操作:
- 在两个相邻的格子上各码上一个方块。
- 在一个格子上码上两个方块。
上述中所提到的所有方块都具有相同的高度。
以下是该游戏的一个图例说明。图中右侧的状态是由图中左侧的状态经过一次上述操作得到,灰色的方块表示操作中新加入的方块。
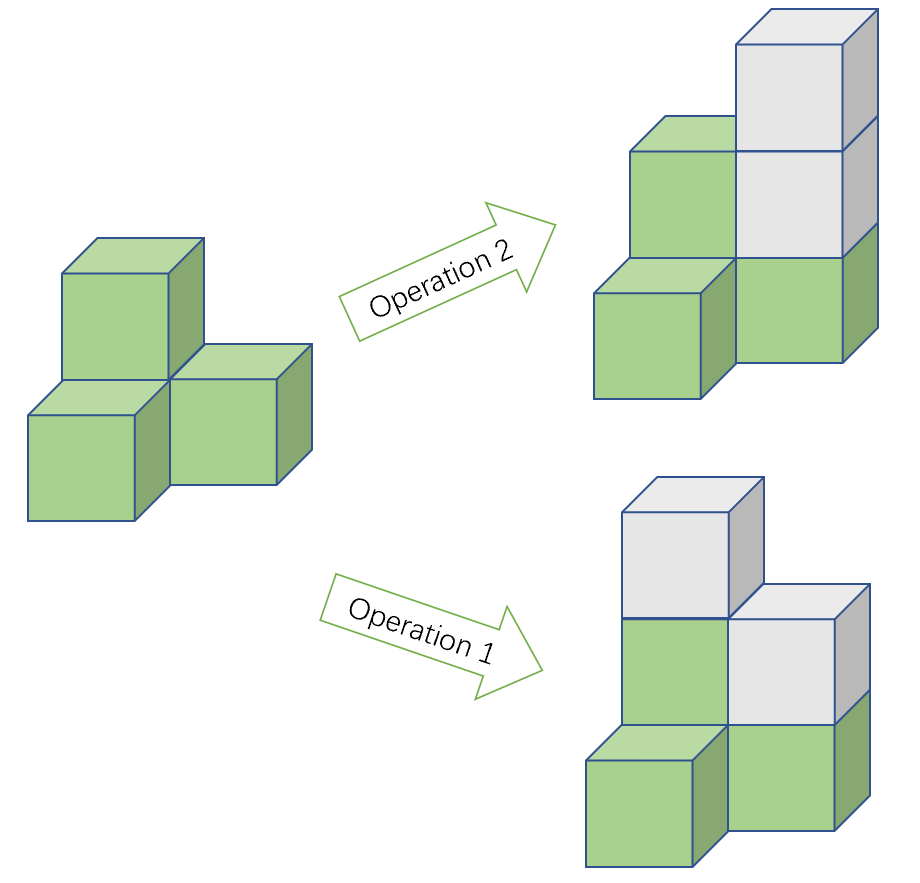
玩家的目标是通过这些操作,使得所有的格子拥有同样的高度(也就是说,每个格子上堆放的方块数相同)。
然而,Alice 发现存在有某些初始局面,使得无论她采用什么策略,都无法达到目标。因此,她希望知道有多少初始局面,满足,
- 对于所有的 $1 \le i \le n$,$1 \le j \le m$,$L \le a_{i, j} \le R$。
- 玩家可以通过执行这些操作,达到目标。
请帮助 Alice 解决这个问题。注意答案可能很大,请输出所求答案对 $998, 244, 353$ 取模的值。
输入格式
无
输出格式
无
说明/提示
在第一个样例中,唯一一种符合要求的初始局面是 $a_{1, 1} = a_{2, 1} = a_{1, 2} = a_{2, 2} = 1$。因此答案为 $1$。
在第二个样例中,符合要求的初始局面有 $a_{1, 1} = a_{1, 2} = 1$ 和 $a_{1, 1} = a_{1, 2} = 2$。因此答案为 $2$。