CF1364D Ehab's Last Corollary
Description
Given a connected undirected graph with $ n $ vertices and an integer $ k $ , you have to either:
- either find an independent set that has exactly $ \lceil\frac{k}{2}\rceil $ vertices.
- or find a simple cycle of length at most $ k $ .
An independent set is a set of vertices such that no two of them are connected by an edge. A simple cycle is a cycle that doesn't contain any vertex twice.
I have a proof that for any input you can always solve at least one of these problems, but it's left as an exercise for the reader.
Input Format
N/A
Output Format
N/A
Explanation/Hint
In the first sample:
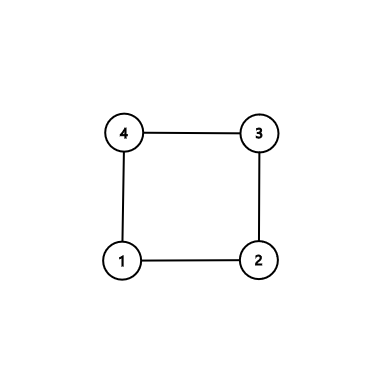
Notice that printing the independent set $ \{2,4\} $ is also OK, but printing the cycle $ 1-2-3-4 $ isn't, because its length must be at most $ 3 $ .
In the second sample:
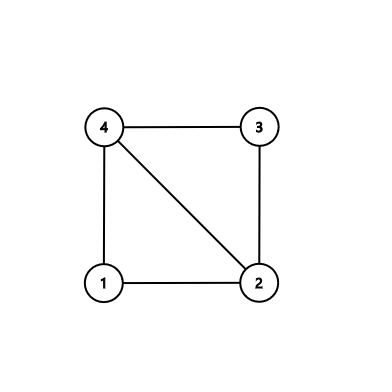
Notice that printing the independent set $ \{1,3\} $ or printing the cycle $ 2-1-4 $ is also OK.
In the third sample:
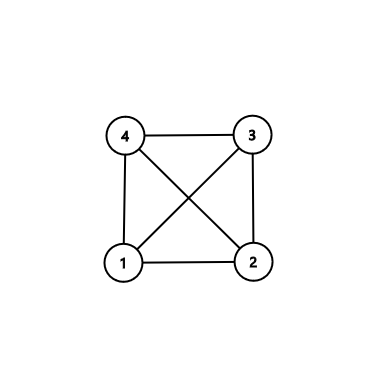
In the fourth sample: