CF1388E Uncle Bogdan and Projections
Description
After returning to shore, uncle Bogdan usually visits the computer club "The Rock", to solve tasks in a pleasant company. One day, uncle Bogdan met his good old friend who told him one unusual task...
There are $ n $ non-intersecting horizontal segments with ends in integers points on the plane with the standard cartesian coordinate system. All segments are strictly above the $ OX $ axis. You can choose an arbitrary vector ( $ a $ , $ b $ ), where $ b < 0 $ and coordinates are real numbers, and project all segments to $ OX $ axis along this vector. The projections shouldn't intersect but may touch each other.
Find the minimum possible difference between $ x $ coordinate of the right end of the rightmost projection and $ x $ coordinate of the left end of the leftmost projection.
Input Format
N/A
Output Format
N/A
Explanation/Hint
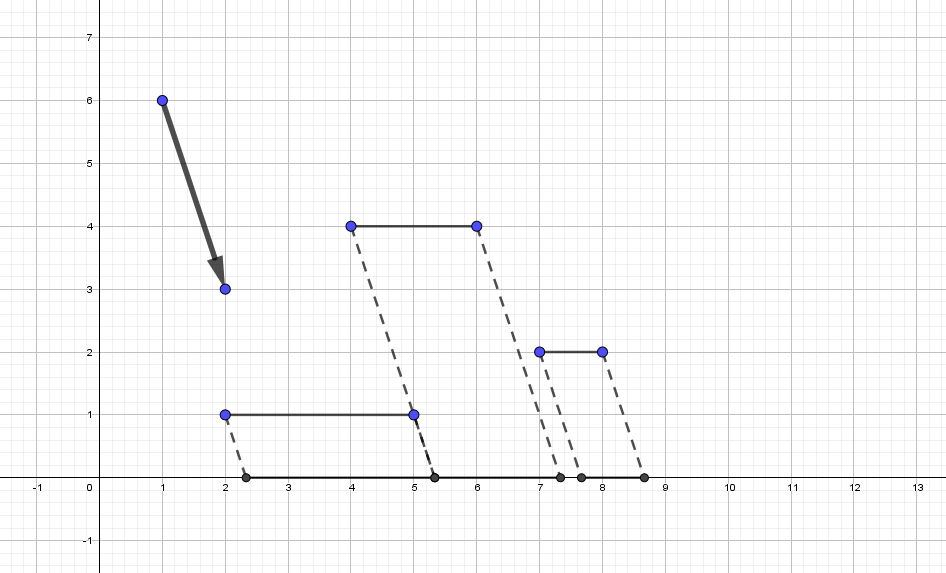
In the first example if we project segments along the vector $ (1, -1) $ then we get an answer $ 12-3=9 $ and (it can be proven) it is impossible to get less.
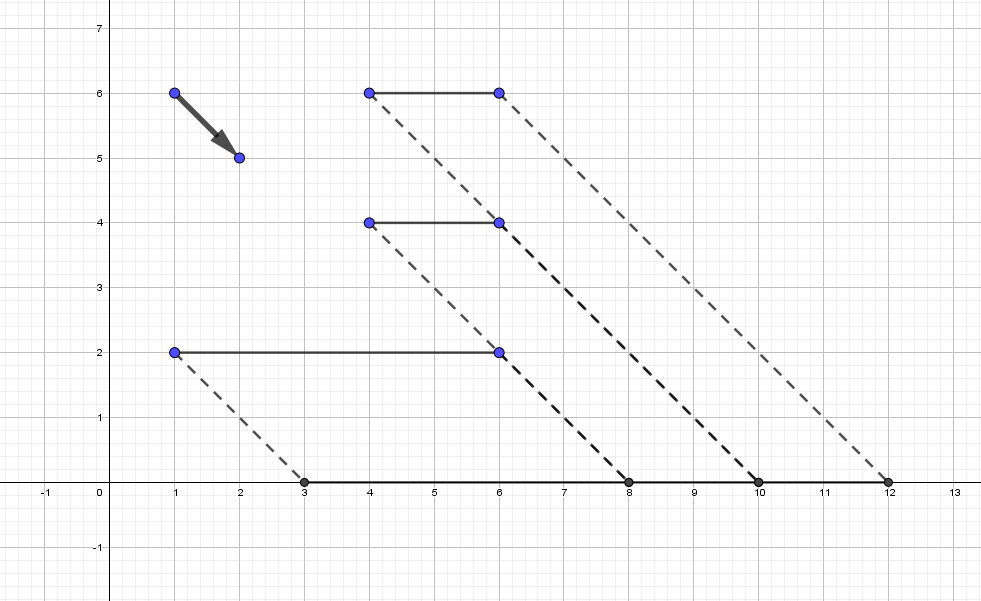It is optimal to project along the vector $ (1, -3) $ in the second example. The answer is $ 8\frac{2}{3}-2\frac{1}{3}=6\frac{1}{3} $