CF1391E Pairs of Pairs

给定一个包含 $n$ 个节点和 $m$ 条边的简单连通无向图。 现在考虑将这 $n$ 个节点中的某些节点两两配对，要求任意一个节点最多只能属于一个配对。 如果对于任意两对配对 $(a, b)$ 和 $(c, d)$，由这四个节点 $\{a, b, c, d\}$ 构成的诱导子图中，最多只有 $2$ 条边（在 $6$ 条可能的边中），则称该配对是合法的。 请注意，诱导子图指的是仅包含该节点集合中的节点，以及两端都在该集合内的边的子图。 现在，请完成以下两种操作之一： - 找出一条包含至少 $ \lceil \frac{n}{2} \rceil $ 个节点的简单路径。这里的简单路径指的是不会重复经过任何节点的路径。 - 找出一个合法配对，使得至少有 $ \lceil \frac{n}{2} \rceil $ 个节点被配对。 可以证明，对于满足题目条件的任意图，至少可以完成上述两种操作之一。

每个测试点包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 10^5$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含两个整数 $n, m$（$2 \le n \le 5 \cdot 10^5$，$1 \le m \le 10^6$），分别表示节点数和边数。 接下来的 $m$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \neq v$），表示在节点 $u$ 和 $v$ 之间有一条无向边。 保证给定的图是连通且简单的——不存在同一对节点之间有多条边，也没有自环。 保证所有测试用例中 $n$ 的总和不超过 $5 \cdot 10^5$。 保证所有测试用例中 $m$ 的总和不超过 $10^6$。

对于每个测试用例，输出格式如下： 如果你找到了一个配对，第一行输出 "PAIRING"（不带引号）。 - 然后输出一个整数 $k$（$ \lceil \frac{n}{2} \rceil \le 2k \le n $），表示配对的对数。 - 接下来 $k$ 行，每行输出两个整数 $a$ 和 $b$，表示 $a$ 和 $b$ 被配对。注意，图中不要求 $a$ 和 $b$ 之间有边！ - 该配对必须是合法的，且每个节点最多只能属于一个配对。 否则，第一行输出 "PATH"（不带引号）。 - 然后输出一个整数 $k$（$ \lceil \frac{n}{2} \rceil \le k \le n $），表示路径上的节点数。 - 第二行输出 $k$ 个整数 $v_1, v_2, \ldots, v_k$，表示路径上节点的顺序。对于每个 $i$（$1 \le i < k$），$v_i$ 和 $v_{i+1}$ 之间有边。 - 该路径必须是简单路径，即每个节点最多出现一次。

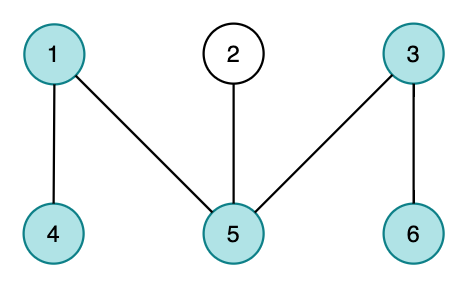
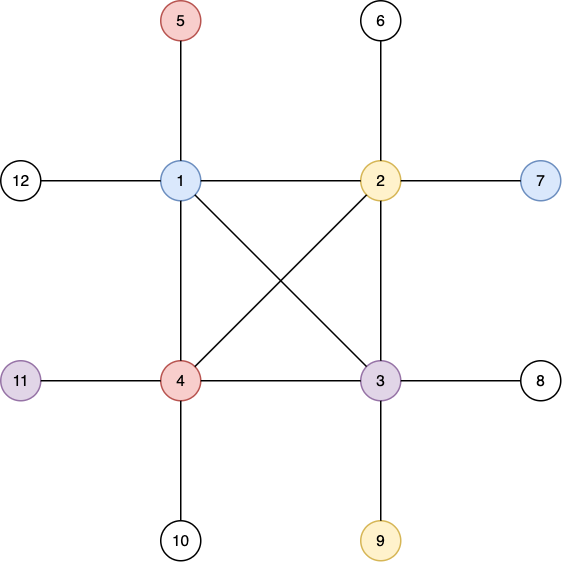
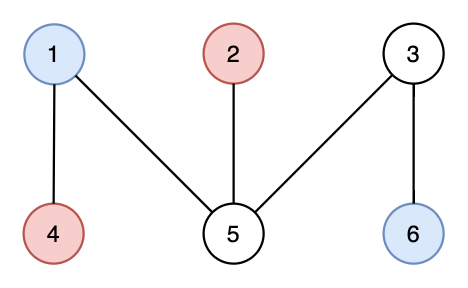
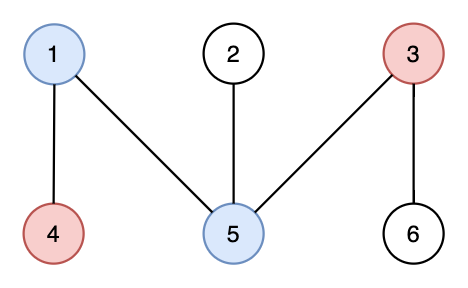
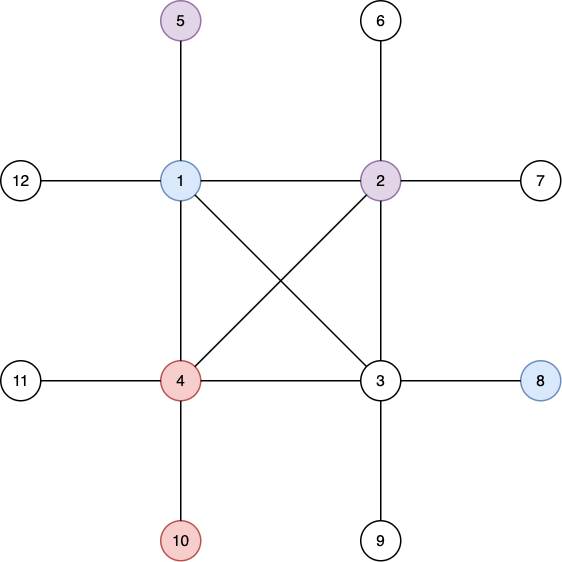
第一种情况下输出的路径如下图所示。  第二种情况下输出的配对如下图所示。  以下是对同一张图的一个不合法配对——诱导子图 $\{1,3,4,5\}$ 有 $3$ 条边。  第三种情况下输出的配对如下图所示。  这是合法的，因为—— - 诱导子图 $\{1,8,2,5\}$ 有边 $(1,2)$ 和 $(1,5)$。 - 诱导子图 $\{1,8,4,10\}$ 有边 $(1,4)$ 和 $(4,10)$。 - 诱导子图 $\{4,10,2,5\}$ 有边 $(2,4)$ 和 $(4,10)$。 第四种情况下输出的配对如下图所示。  由 ChatGPT 4.1 翻译