CF1394B Boboniu Walks on Graph

Boboniu has a directed graph with $ n $ vertices and $ m $ edges. The out-degree of each vertex is at most $ k $ . Each edge has an integer weight between $ 1 $ and $ m $ . No two edges have equal weights. Boboniu likes to walk on the graph with some specific rules, which is represented by a tuple $ (c_1,c_2,\ldots,c_k) $ . If he now stands on a vertex $ u $ with out-degree $ i $ , then he will go to the next vertex by the edge with the $ c_i $ -th $ (1\le c_i\le i) $ smallest weight among all edges outgoing from $ u $ . Now Boboniu asks you to calculate the number of tuples $ (c_1,c_2,\ldots,c_k) $ such that - $ 1\le c_i\le i $ for all $ i $ ( $ 1\le i\le k $ ). - Starting from any vertex $ u $ , it is possible to go back to $ u $ in finite time by walking on the graph under the described rules.

The first line contains three integers $ n $ , $ m $ and $ k $ ( $ 2\le n\le 2\cdot 10^5 $ , $ 2\le m\le \min(2\cdot 10^5,n(n-1) ) $ , $ 1\le k\le 9 $ ). Each of the next $ m $ lines contains three integers $ u $ , $ v $ and $ w $ $ (1\le u,v\le n,u\ne v,1\le w\le m) $ , denoting an edge from $ u $ to $ v $ with weight $ w $ . It is guaranteed that there are no self-loops or multiple edges and each vertex has at least one edge starting from itself. It is guaranteed that the out-degree of each vertex is at most $ k $ and no two edges have equal weight.

Print one integer: the number of tuples.

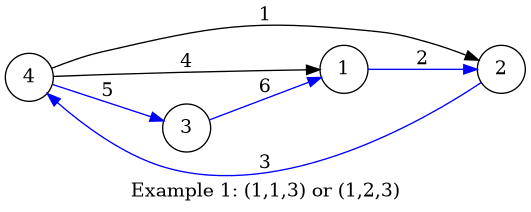
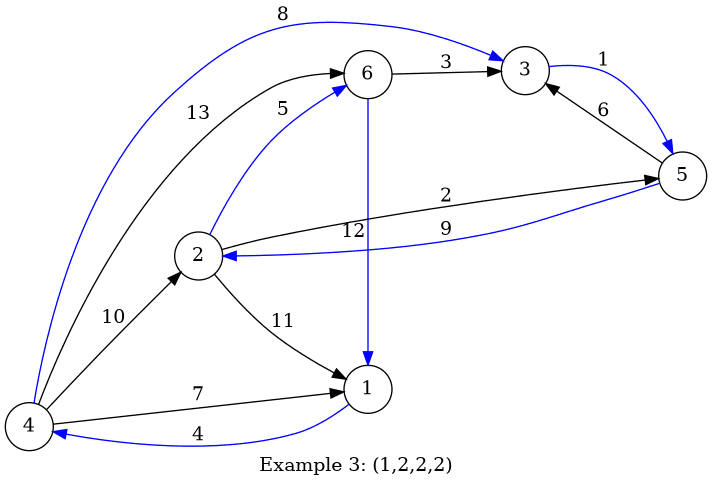
For the first example, there are two tuples: $ (1,1,3) $ and $ (1,2,3) $ . The blue edges in the picture denote the $ c_i $ -th smallest edges for each vertex, which Boboniu chooses to go through. For the third example, there's only one tuple: $ (1,2,2,2) $ . The out-degree of vertex $ u $ means the number of edges outgoing from $ u $ .