CF1508C Complete the MST

As a teacher, Riko Hakozaki often needs to help her students with problems from various subjects. Today, she is asked a programming task which goes as follows. You are given an undirected complete graph with $ n $ nodes, where some edges are pre-assigned with a positive weight while the rest aren't. You need to assign all unassigned edges with non-negative weights so that in the resulting fully-assigned complete graph the [XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR) sum of all weights would be equal to $ 0 $ . Define the ugliness of a fully-assigned complete graph the weight of its [minimum spanning tree](https://en.wikipedia.org/wiki/Minimum_spanning_tree), where the weight of a spanning tree equals the sum of weights of its edges. You need to assign the weights so that the ugliness of the resulting graph is as small as possible. As a reminder, an undirected complete graph with $ n $ nodes contains all edges $ (u, v) $ with $ 1 \le u < v \le n $ ; such a graph has $ \frac{n(n-1)}{2} $ edges. She is not sure how to solve this problem, so she asks you to solve it for her.

N/A

N/A

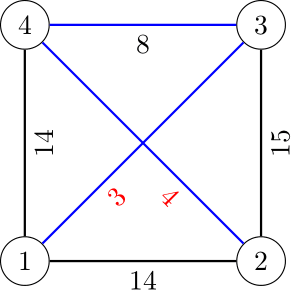
The following image showcases the first test case. The black weights are pre-assigned from the statement, the red weights are assigned by us, and the minimum spanning tree is denoted by the blue edges.