CF1556F Sports Betting

William is not only interested in trading but also in betting on sports matches. $ n $ teams participate in each match. Each team is characterized by strength $ a_i $ . Each two teams $ i < j $ play with each other exactly once. Team $ i $ wins with probability $ \frac{a_i}{a_i + a_j} $ and team $ j $ wins with probability $ \frac{a_j}{a_i + a_j} $ . The team is called a winner if it directly or indirectly defeated all other teams. Team $ a $ defeated (directly or indirectly) team $ b $ if there is a sequence of teams $ c_1 $ , $ c_2 $ , ... $ c_k $ such that $ c_1 = a $ , $ c_k = b $ and team $ c_i $ defeated team $ c_{i + 1} $ for all $ i $ from $ 1 $ to $ k - 1 $ . Note that it is possible that team $ a $ defeated team $ b $ and in the same time team $ b $ defeated team $ a $ . William wants you to find the expected value of the number of winners.

N/A

N/A

To better understand in which situation several winners are possible let's examine the second test: One possible result of the tournament is as follows ( $ a \rightarrow b $ means that $ a $ defeated $ b $ ): - $ 1 \rightarrow 2 $ - $ 2 \rightarrow 3 $ - $ 3 \rightarrow 1 $ - $ 1 \rightarrow 4 $ - $ 1 \rightarrow 5 $ - $ 2 \rightarrow 4 $ - $ 2 \rightarrow 5 $ - $ 3 \rightarrow 4 $ - $ 3 \rightarrow 5 $ - $ 4 \rightarrow 5 $ Or more clearly in the picture: 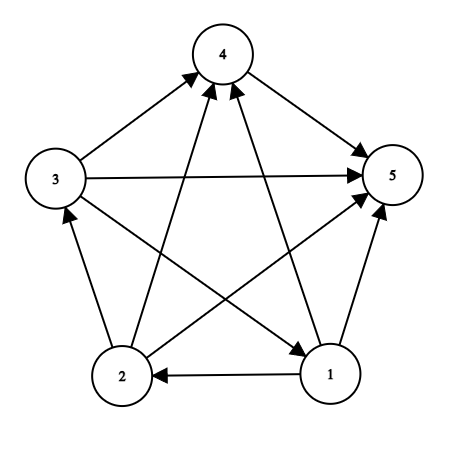In this case every team from the set $ \{ 1, 2, 3 \} $ directly or indirectly defeated everyone. I.e.: - $ 1 $ st defeated everyone because they can get to everyone else in the following way $ 1 \rightarrow 2 $ , $ 1 \rightarrow 2 \rightarrow 3 $ , $ 1 \rightarrow 4 $ , $ 1 \rightarrow 5 $ . - $ 2 $ nd defeated everyone because they can get to everyone else in the following way $ 2 \rightarrow 3 $ , $ 2 \rightarrow 3 \rightarrow 1 $ , $ 2 \rightarrow 4 $ , $ 2 \rightarrow 5 $ . - $ 3 $ rd defeated everyone because they can get to everyone else in the following way $ 3 \rightarrow 1 $ , $ 3 \rightarrow 1 \rightarrow 2 $ , $ 3 \rightarrow 4 $ , $ 3 \rightarrow 5 $ . Therefore the total number of winners is $ 3 $ .