CF1559C Mocha and Hiking

The city where Mocha lives in is called Zhijiang. There are $ n+1 $ villages and $ 2n-1 $ directed roads in this city. There are two kinds of roads: - $ n-1 $ roads are from village $ i $ to village $ i+1 $ , for all $ 1\leq i \leq n-1 $ . - $ n $ roads can be described by a sequence $ a_1,\ldots,a_n $ . If $ a_i=0 $ , the $ i $ -th of these roads goes from village $ i $ to village $ n+1 $ , otherwise it goes from village $ n+1 $ to village $ i $ , for all $ 1\leq i\leq n $ . Mocha plans to go hiking with Taki this weekend. To avoid the trip being boring, they plan to go through every village exactly once. They can start and finish at any villages. Can you help them to draw up a plan?

N/A

N/A

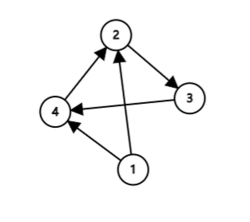
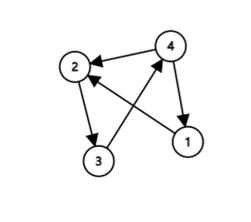
In the first test case, the city looks like the following graph:  So all possible answers are $ (1 \to 4 \to 2 \to 3) $ , $ (1 \to 2 \to 3 \to 4) $ . In the second test case, the city looks like the following graph:  So all possible answers are $ (4 \to 1 \to 2 \to 3) $ , $ (1 \to 2 \to 3 \to 4) $ , $ (3 \to 4 \to 1 \to 2) $ , $ (2 \to 3 \to 4 \to 1) $ .