CF1575K Knitting Batik

Chanek 先生想要编织一块巴迪克（Batik），这是一种来自印度尼西亚的传统布料。这块布料可以看作一个 $n \times m$ 的网格 $a$。共有 $k$ 种颜色，每个格子可以染成 $k$ 种颜色中的一种。 定义子矩形为一对有序的格子 $((x_1, y_1), (x_2, y_2))$，分别表示子矩形在 $a$ 中的左上角和右下角（均包含在内）。两个子矩形 $((x_1, y_1), (x_2, y_2))$ 和 $((x_3, y_3), (x_4, y_4))$ 被认为具有相同的图案，当且仅当满足以下条件： - 它们的宽度相同（$x_2 - x_1 = x_4 - x_3$）； - 它们的高度相同（$y_2 - y_1 = y_4 - y_3$）； - 对于每一对 $(i, j)$，其中 $0 \leq i \leq x_2 - x_1$ 且 $0 \leq j \leq y_2 - y_1$，格子 $(x_1 + i, y_1 + j)$ 和 $(x_3 + i, y_3 + j)$ 的颜色相同。 请计算有多少种可能的巴迪克配色方案，使得子矩形 $((a_x, a_y),(a_x + r - 1, a_y + c - 1))$ 和 $((b_x, b_y),(b_x + r - 1, b_y + c - 1))$ 具有相同的图案。 请将答案对 $10^9 + 7$ 取模后输出。

第一行包含五个整数 $n$、$m$、$k$、$r$ 和 $c$（$1 \leq n, m \leq 10^9$，$1 \leq k \leq 10^9$，$1 \leq r \leq \min(10^6, n)$，$1 \leq c \leq \min(10^6, m)$），分别表示巴迪克的尺寸、颜色数和子矩形的尺寸。 第二行包含四个整数 $a_x$、$a_y$、$b_x$ 和 $b_y$（$1 \leq a_x, b_x \leq n$，$1 \leq a_y, b_y \leq m$），分别表示第一个和第二个子矩形的左上角坐标。保证给定的两个子矩形都在网格内（$1 \leq a_x + r - 1, b_x + r - 1 \leq n$，$1 \leq a_y + c - 1, b_y + c - 1 \leq m$）。

输出一个整数，表示可能的巴迪克配色方案数，对 $10^9 + 7$ 取模。

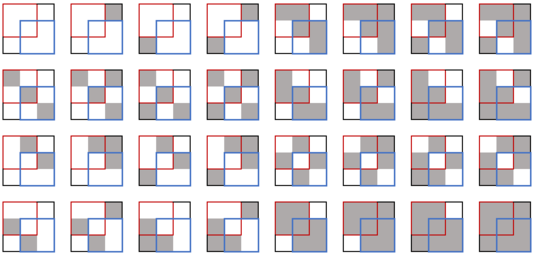
以下是第一个样例中的全部 $32$ 种可能的配色方案。  由 ChatGPT 4.1 翻译