CF1632E2 Distance Tree (hard version)
题目描述
本题与前一题的唯一区别在于 $ n $ 的限制。
一棵树是一个无环连通无向图。加权树的每条边都有一个权值。两个顶点之间的距离是连接它们的路径上所有边权之和的最小值。
给定一棵有 $ n $ 个顶点的加权树,每条边的权值均为 $ 1 $。记 $ d(v) $ 为顶点 $ 1 $ 到顶点 $ v $ 的距离。
定义 $ f(x) $ 为:你可以临时在任意两个顶点 $ a $ 和 $ b $ 之间添加一条权值为 $ x $ 的边($ 1 \le a, b \le n $),此时 $\max\limits_{1 \leq v \leq n} \ {d(v)}$ 的最小可能值。注意,添加这条边后,图不再是一棵树。
对于每个 $ x $ 从 $ 1 $ 到 $ n $,求 $ f(x) $。
输入格式
第一行包含一个整数 $ t $($ 1 \le t \le 10^4 $),表示测试用例的数量。
每个测试用例的第一行包含一个整数 $ n $($ 2 \le n \le 3 \cdot 10^5 $)。
接下来的 $ n-1 $ 行,每行包含两个整数 $ u $ 和 $ v $($ 1 \le u,v \le n $),表示在顶点 $ u $ 和 $ v $ 之间有一条边。保证给定的边构成一棵树。
保证所有测试用例中 $ n $ 的总和不超过 $ 3 \cdot 10^5 $。
输出格式
对于每个测试用例,输出 $ n $ 个整数,依次表示 $ f(1), f(2), \ldots, f(n) $,用空格隔开。
说明/提示
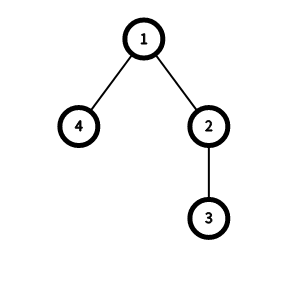
在第一个测试用例中:
- 对于 $ x = 1 $,可以在顶点 $ 1 $ 和 $ 3 $ 之间添加一条边,此时 $ d(1) = 0 $,$ d(2) = d(3) = d(4) = 1 $,所以 $ f(1) = 1 $。
- 对于 $ x \ge 2 $,无论添加哪条边,$ d(1) = 0 $,$ d(2) = d(4) = 1 $,$ d(3) = 2 $,所以 $ f(x) = 2 $。
由 ChatGPT 4.1 翻译