CF1665C Tree Infection

A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. The parent of a vertex $ v $ (different from root) is the previous to $ v $ vertex on the shortest path from the root to the vertex $ v $ . Children of the vertex $ v $ are all vertices for which $ v $ is the parent. You are given a rooted tree with $ n $ vertices. The vertex $ 1 $ is the root. Initially, all vertices are healthy. Each second you do two operations, the spreading operation and, after that, the injection operation: 1. Spreading: for each vertex $ v $ , if at least one child of $ v $ is infected, you can spread the disease by infecting at most one other child of $ v $ of your choice. 2. Injection: you can choose any healthy vertex and infect it. This process repeats each second until the whole tree is infected. You need to find the minimal number of seconds needed to infect the whole tree.

N/A

N/A

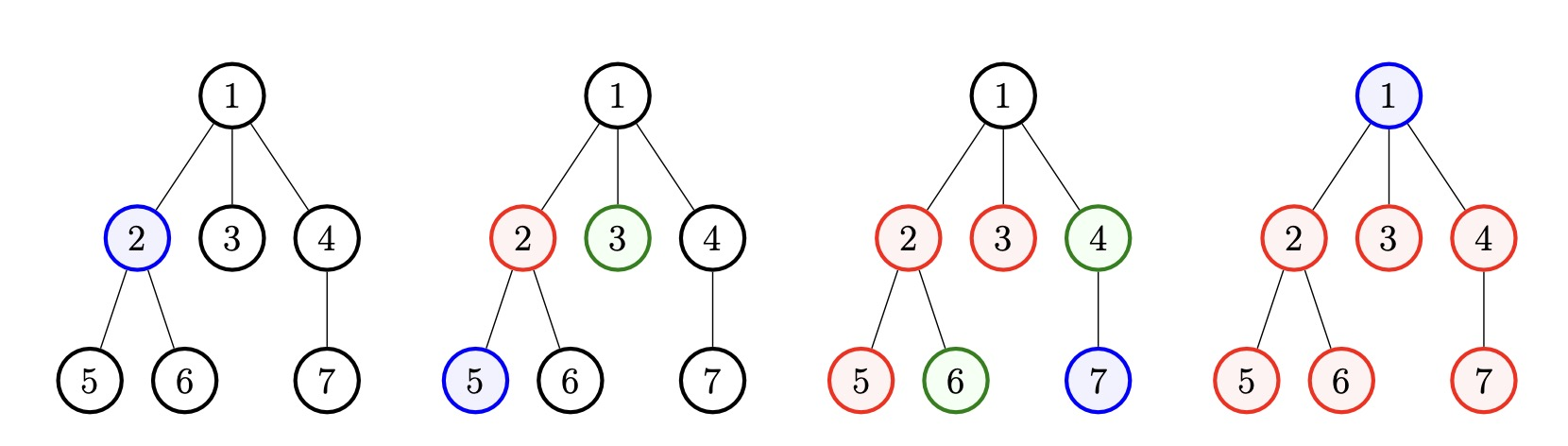The image depicts the tree from the first test case during each second. A vertex is black if it is not infected. A vertex is blue if it is infected by injection during the previous second. A vertex is green if it is infected by spreading during the previous second. A vertex is red if it is infected earlier than the previous second. Note that you are able to choose which vertices are infected by spreading and by injections.