CF1714G Path Prefixes

You are given a rooted tree. It contains $ n $ vertices, which are numbered from $ 1 $ to $ n $ . The root is the vertex $ 1 $ . Each edge has two positive integer values. Thus, two positive integers $ a_j $ and $ b_j $ are given for each edge. Output $ n-1 $ numbers $ r_2, r_3, \dots, r_n $ , where $ r_i $ is defined as follows. Consider the path from the root (vertex $ 1 $ ) to $ i $ ( $ 2 \le i \le n $ ). Let the sum of the costs of $ a_j $ along this path be $ A_i $ . Then $ r_i $ is equal to the length of the maximum prefix of this path such that the sum of $ b_j $ along this prefix does not exceed $ A_i $ . 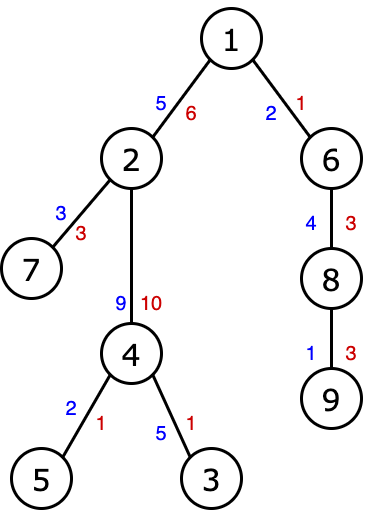Example for $ n=9 $ . The blue color shows the costs of $ a_j $ , and the red color shows the costs of $ b_j $ .Consider an example. In this case: - $ r_2=0 $ , since the path to $ 2 $ has an amount of $ a_j $ equal to $ 5 $ , only the prefix of this path of length $ 0 $ has a smaller or equal amount of $ b_j $ ; - $ r_3=3 $ , since the path to $ 3 $ has an amount of $ a_j $ equal to $ 5+9+5=19 $ , the prefix of length $ 3 $ of this path has a sum of $ b_j $ equal to $ 6+10+1=17 $ ( the number is $ 17 \le 19 $ ); - $ r_4=1 $ , since the path to $ 4 $ has an amount of $ a_j $ equal to $ 5+9=14 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 6 $ (this is the longest suitable prefix, since the prefix of length $ 2 $ already has an amount of $ b_j $ equal to $ 6+10=16 $ , which is more than $ 14 $ ); - $ r_5=2 $ , since the path to $ 5 $ has an amount of $ a_j $ equal to $ 5+9+2=16 $ , the prefix of length $ 2 $ of this path has a sum of $ b_j $ equal to $ 6+10=16 $ (this is the longest suitable prefix, since the prefix of length $ 3 $ already has an amount of $ b_j $ equal to $ 6+10+1=17 $ , what is more than $ 16 $ ); - $ r_6=1 $ , since the path up to $ 6 $ has an amount of $ a_j $ equal to $ 2 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 1 $ ; - $ r_7=1 $ , since the path to $ 7 $ has an amount of $ a_j $ equal to $ 5+3=8 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 6 $ (this is the longest suitable prefix, since the prefix of length $ 2 $ already has an amount of $ b_j $ equal to $ 6+3=9 $ , which is more than $ 8 $ ); - $ r_8=2 $ , since the path up to $ 8 $ has an amount of $ a_j $ equal to $ 2+4=6 $ , the prefix of length $ 2 $ of this path has an amount of $ b_j $ equal to $ 1+3=4 $ ; - $ r_9=3 $ , since the path to $ 9 $ has an amount of $ a_j $ equal to $ 2+4+1=7 $ , the prefix of length $ 3 $ of this path has a sum of $ b_j $ equal to $ 1+3+3=7 $ .

N/A

N/A

The first example is clarified in the statement. In the second example: - $ r_2=0 $ , since the path to $ 2 $ has an amount of $ a_j $ equal to $ 1 $ , only the prefix of this path of length $ 0 $ has a smaller or equal amount of $ b_j $ ; - $ r_3=0 $ , since the path to $ 3 $ has an amount of $ a_j $ equal to $ 1+1=2 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 100 $ ( $ 100 > 2 $ ); - $ r_4=3 $ , since the path to $ 4 $ has an amount of $ a_j $ equal to $ 1+1+101=103 $ , the prefix of length $ 3 $ of this path has an amount of $ b_j $ equal to $ 102 $ , .