CF1763F Edge Queries

You are given an undirected, connected graph of $ n $ nodes and $ m $ edges. All nodes $ u $ of the graph satisfy the following: - Let $ S_u $ be the set of vertices in the longest simple cycle starting and ending at $ u $ . - Let $ C_u $ be the union of the sets of vertices in any simple cycle starting and ending at $ u $ . - $ S_u = C_u $ . You need to answer $ q $ queries. For each query, you will be given node $ a $ and node $ b $ . Out of all the edges that belong to any simple path from $ a $ to $ b $ , count the number of edges such that if you remove that edge, $ a $ and $ b $ are reachable from each other.

N/A

N/A

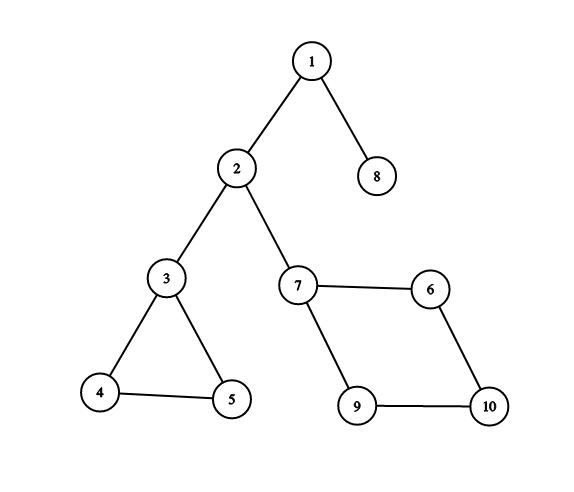The graph in the first sample is : The first query is $ (1, 4) $ . There are $ 5 $ total edges that belong to any simple path from $ 1 $ to $ 4 $ . Edges $ (3, 4), (4, 5), (5, 3) $ will be counted in the answer to the query. The fourth query is $ (2, 8) $ . There is only one simple path from $ 2 $ to $ 8 $ , thus none of the edges will be counted in the answer to the query. The fifth query is $ (7, 10) $ . There are $ 4 $ total edges that belong to any simple path from $ 7 $ to $ 10 $ , all of them will be counted in the answer to the query.