CF1878G wxhtzdy ORO Tree

After (finally) qualifying for the IOI 2023, wxhtzdy was very happy, so he decided to do what most competitive programmers do: trying to guess the problems that will be on IOI. During this process, he accidentally made a problem, which he thought was really cool. You are given a tree (a connected acyclic graph) with $ n $ vertices and $ n-1 $ edges. Vertex $ i $ ( $ 1 \le i \le n $ ) has a value $ a_i $ . Lets' define $ g(u, v) $ as the [bitwise or](http://tiny.cc/bitwise_or) of the values of all vertices on the shortest path from $ u $ to $ v $ . For example, let's say that we want to calculate $ g(3, 4) $ , on the tree from the first test case in the example. On the path from $ 3 $ to $ 4 $ are vertices $ 3 $ , $ 1 $ , $ 4 $ . Then, $ g(3, 4) = a_3 \ | \ a_1 \ | \ a_4 $ (here, $ | $ represents the [bitwise OR operation](http://tiny.cc/bitwise_or)). Also, you are given $ q $ queries, and each query looks like this: You are given $ x $ and $ y $ . Let's consider all vertices $ z $ such that $ z $ is on the shortest path from $ x $ to $ y $ (inclusive). Lets define the niceness of a vertex $ z $ as the sum of the number of non-zero bits in $ g(x, z) $ and the number of non-zero bits in $ g(y, z) $ . You need to find the maximum niceness among all vertices $ z $ on the shortest path from $ x $ to $ y $ . Since his brain is really tired after solving an output only problem on SIO (he had to do it to qualify for the IOI), he wants your help with this problem.

N/A

N/A

The image below shows the tree from the second example, first test case. 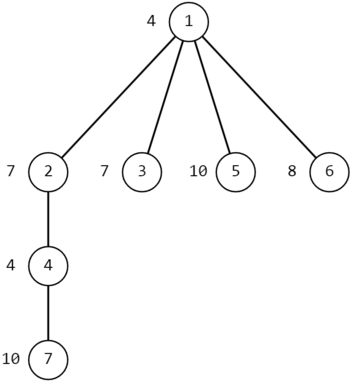 Tree from the second example, first test caseIn the first query, we have $ x=7 $ , $ y=5 $ . The shortest path from $ 7 $ to $ 5 $ is $ 7-4-2-1-5 $ . Let's calculate the niceness of vertex $ 7 $ on this path. We have $ g(7,7)=a_7=10=(1010)_2 $ and $ g(5,7)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4 \ | \ a_7=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2 $ , so its niceness is equal to $ 2 + 4 = 6 $ . Now let's calculate the niceness of vertex $ 4 $ on this path. We have $ g(7,4)=a_7 \ | \ a_4=10 \ | \ 4=14=(1110)_2 $ and $ g(5,4)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2 $ , so its niceness is equal to $ 3 + 4 = 7 $ . Now let's calculate the niceness of vertex $ 2 $ on this path. We have $ g(7,2)=a_7 \ | \ a_4 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2 $ and $ g(5,2)=a_5 \ | \ a_1 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2 $ , so its niceness is equal to $ 4 + 4 = 8 $ . Now let's calculate the niceness of vertex $ 1 $ on this path. We have $ g(7,1)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2 $ and $ g(5,1)=a_5 \ | \ a_1=10 \ | \ 4=14=(1110)_2 $ , so its niceness is equal to $ 4 + 3 = 7 $ . Finally, let's calculate the niceness of vertex $ 5 $ on this path. We have $ g(7,5)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1 \ | \ a_5=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2 $ and $ g(5,5)=a_5=10=(1010)_2 $ , so its niceness is equal to $ 4 + 2 = 6 $ . The maximum niceness on this path is at vertex $ 2 $ , and it is $ 8 $ .