CF195E Building Forest

### 题意翻译 一个有向加权森林是无环有向加权图，其中每个顶点至多有一条边。有向加权森林中，顶点 $ v $ 的根是一个没有出边的顶点，并且可以通过沿着加权有向森林的边从顶点 $ v $ 到达。现将顶点 $ v $ 的根记为 $ root(v) $。顶点v的深度是从顶点 $ v $ 到其根的路径的权重之和。现将顶点 $ v $ 的深度表示为 $ depth(v) $。 构建加权定向森林的过程如下：最初，森林不包含顶点。顶点按顺序逐个添加。总体而言，有 $ n $ 个执行的加法操作。 第 $ i（i>0）$个 操作由一组数字 （$ k $,$ v1 $，$ x1 $，$ v2 $， $ x2 $， ... $ vk $，$ xk $） 描述，意味着我们应该将顶点 $ i $ 下的边 $ k $ 添加到图中。 从顶点 $root( v_1 )$ 到顶点$ i $的边，权重为 $depth( v_1 ) + x_1 $；从顶点 $root( v2 )$ 到顶点$ i $的边，权重为 $ depth( v2 ) +  x2 $ ，以此类推。如果 $ k=0 $，那么图中只增加了顶点 $ i $ ，没有增加任何边。 现给定添加的顶点，请计算森林所有边的权重之和。由于数据可能很大，请将输出的数据模 $1000000007$ $（10^9 + 7）$。

无

无

Conside the first sample: 1. Vertex $ 1 $ is added. $ k=0 $ , thus no edges are added. 2. Vertex $ 2 $ is added. $ k=0 $ , thus no edges are added. 3. Vertex $ 3 $ is added. $ k=1 $ . $ v_{1}=2 $ , $ x_{1}=1 $ . Edge from vertex $ root(2)=2 $ to vertex $ 3 $ with weight $ depth(2)+x_{1}=0+1=1 $ is added. 4. Vertex $ 4 $ is added. $ k=2 $ . $ v_{1}=1 $ , $ x_{1}=5 $ . Edge from vertex $ root(1)=1 $ to vertex $ 4 $ with weight $ depth(1)+x_{1}=0+5=5 $ is added. $ v_{2}=2 $ , $ x_{2}=2 $ . Edge from vertex $ root(2)=3 $ to vertex $ 4 $ with weight $ depth(2)+x_{1}=1+2=3 $ is added. 5. Vertex $ 5 $ is added. $ k=1 $ . $ v_{1}=1 $ , $ x_{1}=2 $ . Edge from vertex $ root(1)=4 $ to vertex $ 5 $ with weight $ depth(1)+x_{1}=5+2=7 $ is added. 6. Vertex $ 6 $ is added. $ k=1 $ . $ v_{1}=3 $ , $ x_{1}=4 $ . Edge from vertex $ root(3)=5 $ to vertex $ 6 $ with weight $ depth(3)+x_{1}=10+4=14 $ is added. 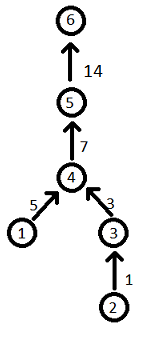The resulting graph is shown on the pictore below: