CF232B Table

John Doe has an $ n×m $ table. John Doe can paint points in some table cells, not more than one point in one table cell. John Doe wants to use such operations to make each square subtable of size $ n×n $ have exactly $ k $ points. John Doe wondered, how many distinct ways to fill the table with points are there, provided that the condition must hold. As this number can be rather large, John Doe asks to find its remainder after dividing by $ 1000000007 $ $ (10^{9}+7) $ . You should assume that John always paints a point exactly in the center of some cell. Two ways to fill a table are considered distinct, if there exists a table cell, that has a point in one way and doesn't have it in the other.

N/A

N/A

Let's consider the first test case: 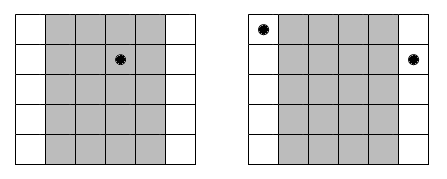 The gray area belongs to both $ 5×5 $ squares. So, if it has one point, then there shouldn't be points in any other place. If one of the white areas has a point, then the other one also must have a point. Thus, there are about $ 20 $ variants, where the point lies in the gray area and $ 25 $ variants, where each of the white areas contains a point. Overall there are $ 45 $ variants.