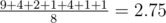CF235B Let's Play Osu!
Description
You're playing a game called Osu! Here's a simplified version of it. There are $ n $ clicks in a game. For each click there are two outcomes: correct or bad. Let us denote correct as "O", bad as "X", then the whole play can be encoded as a sequence of $ n $ characters "O" and "X".
Using the play sequence you can calculate the score for the play as follows: for every maximal consecutive "O"s block, add the square of its length (the number of characters "O") to the score. For example, if your play can be encoded as "OOXOOOXXOO", then there's three maximal consecutive "O"s block "OO", "OOO", "OO", so your score will be $ 2^{2}+3^{2}+2^{2}=17 $ . If there are no correct clicks in a play then the score for the play equals to $ 0 $ .
You know that the probability to click the $ i $ -th $ (1
Input Format
N/A
Output Format
N/A
Explanation/Hint
For the first example. There are 8 possible outcomes. Each has a probability of 0.125.
- "OOO" $ → $ $ 3^{2}=9 $ ;
- "OOX" $ → $ $ 2^{2}=4 $ ;
- "OXO" $ → $ $ 1^{2}+1^{2}=2 $ ;
- "OXX" $ → $ $ 1^{2}=1 $ ;
- "XOO" $ → $ $ 2^{2}=4 $ ;
- "XOX" $ → $ $ 1^{2}=1 $ ;
- "XXO" $ → $ $ 1^{2}=1 $ ;
- "XXX" $ → $ $ 0 $ .
So the expected score is 