CF321E Ciel and Gondolas

Fox Ciel is in the Amusement Park. And now she is in a queue in front of the Ferris wheel. There are $ n $ people (or foxes more precisely) in the queue: we use first people to refer one at the head of the queue, and $ n $ -th people to refer the last one in the queue. There will be $ k $ gondolas, and the way we allocate gondolas looks like this: - When the first gondolas come, the $ q_{1} $ people in head of the queue go into the gondolas. - Then when the second gondolas come, the $ q_{2} $ people in head of the remain queue go into the gondolas. ... - The remain $ q_{k} $ people go into the last ( $ k $ -th) gondolas. Note that $ q_{1} $ , $ q_{2} $ , ..., $ q_{k} $ must be positive. You can get from the statement that 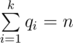 and $ q_{i}>0 $ . You know, people don't want to stay with strangers in the gondolas, so your task is to find an optimal allocation way (that is find an optimal sequence $ q $ ) to make people happy. For every pair of people $ i $ and $ j $ , there exists a value $ u_{ij} $ denotes a level of unfamiliar. You can assume $ u_{ij}=u_{ji} $ for all $ i,j $ $ (1

N/A

N/A

In the first example, we can allocate people like this: {1, 2} goes into a gondolas, {3, 4, 5} goes into another gondolas. In the second example, an optimal solution is : {1, 2, 3} | {4, 5, 6} | {7, 8}.