CF337E Divisor Tree

A divisor tree is a rooted tree that meets the following conditions: - Each vertex of the tree contains a positive integer number. - The numbers written in the leaves of the tree are prime numbers. - For any inner vertex, the number within it is equal to the product of the numbers written in its children. Manao has $ n $ distinct integers $ a_{1},a_{2},...,a_{n} $ . He tries to build a divisor tree which contains each of these numbers. That is, for each $ a_{i} $ , there should be at least one vertex in the tree which contains $ a_{i} $ . Manao loves compact style, but his trees are too large. Help Manao determine the minimum possible number of vertices in the divisor tree sought.

N/A

N/A

Sample 1. The smallest divisor tree looks this way: 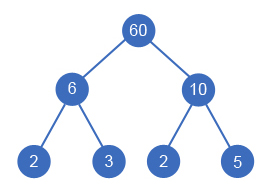 Sample 2. In this case you can build the following divisor tree: 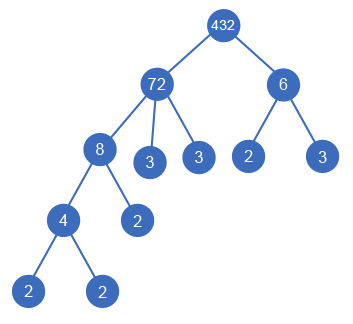 Sample 3. Note that the tree can consist of a single vertex.