CF359C Prime Number

Simon has a prime number $ x $ and an array of non-negative integers $ a_{1},a_{2},...,a_{n} $ . Simon loves fractions very much. Today he wrote out number 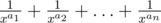 on a piece of paper. After Simon led all fractions to a common denominator and summed them up, he got a fraction: , where number $ t $ equals $ x^{a_{1}+a_{2}+...+a_{n}} $ . Now Simon wants to reduce the resulting fraction. Help him, find the greatest common divisor of numbers $ s $ and $ t $ . As GCD can be rather large, print it as a remainder after dividing it by number $ 1000000007 $ ( $ 10^{9}+7 $ ).

N/A

N/A

In the first sample 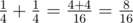. Thus, the answer to the problem is $ 8 $ . In the second sample, 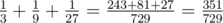. The answer to the problem is $ 27 $ , as $ 351=13·27 $ , $ 729=27·27 $ . In the third sample the answer to the problem is $ 1073741824 mod 1000000007=73741817 $ . In the fourth sample 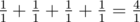. Thus, the answer to the problem is $ 1 $ .