CF388D Fox and Perfect Sets

Fox Ciel studies number theory. She thinks a non-empty set $ S $ contains non-negative integers is perfect if and only if for any 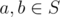 ( $ a $ can be equal to $ b $ ), 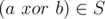. Where operation $ xor $ means exclusive or operation (http://en.wikipedia.org/wiki/Exclusive\_or). Please calculate the number of perfect sets consisting of integers not greater than $ k $ . The answer can be very large, so print it modulo $ 1000000007 $ $ (10^{9}+7) $ .

N/A

N/A

In example 1, there are 2 such sets: {0} and {0, 1}. Note that {1} is not a perfect set since 1 xor 1 = 0 and {1} doesn't contain zero. In example 4, there are 6 such sets: {0}, {0, 1}, {0, 2}, {0, 3}, {0, 4} and {0, 1, 2, 3}.