CF431C k-Tree

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a $ k $ -tree. A $ k $ -tree is an infinite rooted tree where: - each vertex has exactly $ k $ children; - each edge has some weight; - if we look at the edges that goes from some vertex to its children (exactly $ k $ edges), then their weights will equal $ 1,2,3,...,k $ . The picture below shows a part of a 3-tree.  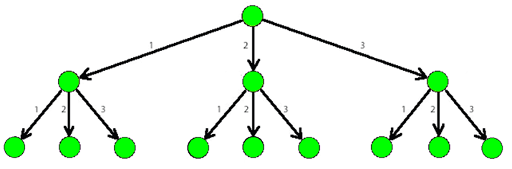As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: "How many paths of total weight $ n $ (the sum of all weights of the edges in the path) are there, starting from the root of a $ k $ -tree and also containing at least one edge of weight at least $ d $ ?".Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo $ 1000000007 $ ( $ 10^{9}+7 $ ).

N/A

N/A