Berland Miners

Berland有一个山洞组成的树。每个山洞有一个高度。这棵树有一个根。所以，每个山洞都有一条从 根到这个山洞的路径。你现在有K个货物要从根部运到山洞中去，且任意两个货物不能到达同一个节点。每个货物都有一个高度h[i]，所 以这个货物经过的所有山洞，都不能低于h[i]。 你现在可以改变一个山洞的高度。问最少增加多少，使得所有货物都能运到山洞中去。 数据范围5e5. 感谢@可爱即是正义 提供的翻译

The biggest gold mine in Berland consists of $ n $ caves, connected by $ n-1 $ transitions. The entrance to the mine leads to the cave number $ 1 $ , it is possible to go from it to any remaining cave of the mine by moving along the transitions. The mine is being developed by the InMine Inc., $ k $ miners work for it. Each day the corporation sorts miners into caves so that each cave has at most one miner working there. For each cave we know the height of its ceiling $ h_{i} $ in meters, and for each miner we know his height $ s_{j} $ , also in meters. If a miner's height doesn't exceed the height of the cave ceiling where he is, then he can stand there comfortably, otherwise, he has to stoop and that makes him unhappy. Unfortunately, miners typically go on strike in Berland, so InMine makes all the possible effort to make miners happy about their work conditions. To ensure that no miner goes on strike, you need make sure that no miner has to stoop at any moment on his way from the entrance to the mine to his cave (in particular, he must be able to stand comfortably in the cave where he works). To reach this goal, you can choose exactly one cave and increase the height of its ceiling by several meters. However enlarging a cave is an expensive and complex procedure. That's why InMine Inc. asks you either to determine the minimum number of meters you should raise the ceiling of some cave so that it is be possible to sort the miners into the caves and keep all miners happy with their working conditions or to determine that it is impossible to achieve by raising ceiling in exactly one cave.

The first line contains integer $ n $ ( $ 1<=n<=5·10^{5} $ ) — the number of caves in the mine. Then follows a line consisting of $ n $ positive integers $ h_{1},h_{2},...,h_{n} $ ( $ 1<=h_{i}<=10^{9} $ ), where $ h_{i} $ is the height of the ceiling in the $ i $ -th cave. Next $ n-1 $ lines contain the descriptions of transitions between the caves. Each line has the form $ a_{i},b_{i} $ ( $ 1<=a_{i},b_{i}<=n $ , $ a_{i}≠b_{i} $ ), where $ a_{i} $ and $ b_{i} $ are the numbers of the caves connected by a path. The next line contains integer $ k $ ( $ 1<=k<=n $ ). The last line contains $ k $ integers $ s_{1},s_{2},...,s_{k} $ ( $ 1<=s_{j}<=10^{9} $ ), where $ s_{j} $ is the $ j $ -th miner's height.

In the single line print the minimum number of meters that you need to raise the ceiling by in some cave so that all miners could be sorted into caves and be happy about the work conditions. If it is impossible to do, print $ -1 $ . If it is initially possible and there's no need to raise any ceiling, print $ 0 $ .

6
5 8 4 6 3 12
1 2
1 3
4 2
2 5
6 3
6
7 4 2 5 3 11

6

7
10 14 7 12 4 50 1
1 2
2 3
2 4
5 1
6 5
1 7
6
7 3 4 8 8 10

0

3
4 2 8
1 2
1 3
2
17 15

-1

In the first sample test we should increase ceiling height in the first cave from $ 5 $ to $ 11 $ . After that we can distribute miners as following (first goes index of a miner, then index of a cave): 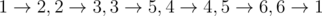. In the second sample test there is no need to do anything since it is already possible to distribute miners as following: 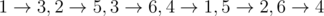. In the third sample test it is impossible.