CF549E Sasha Circle

Berlanders like to eat cones after a hard day. Misha Square and Sasha Circle are local authorities of Berland. Each of them controls its points of cone trade. Misha has $ n $ points, Sasha — $ m $ . Since their subordinates constantly had conflicts with each other, they decided to build a fence in the form of a circle, so that the points of trade of one businessman are strictly inside a circle, and points of the other one are strictly outside. It doesn't matter which of the two gentlemen will have his trade points inside the circle. Determine whether they can build a fence or not.

N/A

N/A

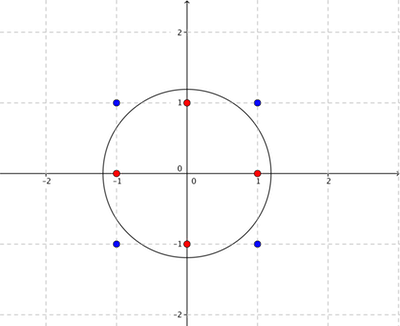
In the first sample there is no possibility to separate points, because any circle that contains both points $ (-1,0),(1,0) $ also contains at least one point from the set $ (0,-1),(0,1) $ , and vice-versa: any circle that contains both points $ (0,-1),(0,1) $ also contains at least one point from the set $ (-1,0),(1,0) $ In the second sample one of the possible solution is shown below. Misha's points are marked with red colour and Sasha's are marked with blue.