Kleofáš and the n-thlon
题意翻译
$m$ 个人参加 $n$ 项比赛。
每场比赛有一个分值,在 $[1,m]$ 之间,且同一场比赛每个人的得分两两不同。总分为每场比赛得分之和。
有一个人,给出他每场比赛的得分 $c_i$ 求这个人总分排名(第几小)的期望值。
排名的定义为 $1+k$, $k$ 表示总分严格比他低的人数。
$n \leq 100$,$m \leq 10^3$。
题目描述
Kleofáš is participating in an $ n $ -thlon - a tournament consisting of $ n $ different competitions in $ n $ different disciplines (numbered $ 1 $ through $ n $ ). There are $ m $ participants in the $ n $ -thlon and each of them participates in all competitions.
In each of these $ n $ competitions, the participants are given ranks from $ 1 $ to $ m $ in such a way that no two participants are given the same rank - in other words, the ranks in each competition form a permutation of numbers from $ 1 $ to $ m $ . The score of a participant in a competition is equal to his/her rank in it.
The overall score of each participant is computed as the sum of that participant's scores in all competitions.
The overall rank of each participant is equal to $ 1+k $ , where $ k $ is the number of participants with strictly smaller overall score.
The $ n $ -thlon is over now, but the results haven't been published yet. Kleofáš still remembers his ranks in each particular competition; however, he doesn't remember anything about how well the other participants did. Therefore, Kleofáš would like to know his expected overall rank.
All competitors are equally good at each discipline, so all rankings (permutations of ranks of everyone except Kleofáš) in each competition are equiprobable.
输入输出格式
输入格式
The first line of the input contains two space-separated integers $ n $ ( $ 1<=n<=100 $ ) and $ m $ ( $ 1<=m<=1000 $ ) — the number of competitions and the number of participants respectively.
Then, $ n $ lines follow. The $ i $ -th of them contains one integer $ x_{i} $ ( $ 1<=x_{i}<=m $ ) — the rank of Kleofáš in the $ i $ -th competition.
输出格式
Output a single real number – the expected overall rank of Kleofáš. Your answer will be considered correct if its relative or absolute error doesn't exceed $ 10^{-9} $ .
Namely: let's assume that your answer is $ a $ , and the answer of the jury is $ b $ . The checker program will consider your answer correct, if 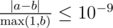.
输入输出样例
输入样例 #1
4 10
2
1
2
1
输出样例 #1
1.0000000000000000
输入样例 #2
5 5
1
2
3
4
5
输出样例 #2
2.7500000000000000
输入样例 #3
3 6
2
4
2
输出样例 #3
1.6799999999999999
说明
In the first sample, Kleofáš has overall score $ 6 $ . Nobody else can have overall score less than $ 6 $ (but it's possible for one other person to have overall score $ 6 $ as well), so his overall rank must be $ 1 $ .