CF689D Friends and Subsequences
Description
Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?
Every one of them has an integer sequences $ a $ and $ b $ of length $ n $ . Being given a query of the form of pair of integers $ (l,r) $ , Mike can instantly tell the value of 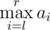 while !Mike can instantly tell the value of 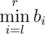.
Now suppose a robot (you!) asks them all possible different queries of pairs of integers $ (l,r) $ $ (1
Input Format
N/A
Output Format
N/A
Explanation/Hint
The occasions in the first sample case are:
1\. $ l=4 $ , $ r=4 $ since $ max{2}=min{2} $ .
2\. $ l=4 $ , $ r=5 $ since $ max{2,1}=min{2,3} $ .
There are no occasions in the second sample case since Mike will answer $ 3 $ to any query pair, but !Mike will always answer $ 1 $ .