CF698F Coprime Permutation
题目描述
当且仅当两个正整数没有大于 $1$ 的公约数时,这两个数互质。
有只熊不想告诉 Radewoosh 怎么解决某道算法题。因此,Radewoosh 打算闯进这只熊藏有解答的保险箱中。为了通过那道门,他需要输入 $1$ 到 $n$ 的一个排列。门只有在输入的排列 $p_{1},p_{2},...,p_{n}$ 满足如下条件时才会打开:
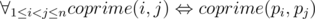
换句话说,当且仅当两个下标互质时,对应的两个数也互质。
排列中的部分值可能已经被确定。Radewoosh 要有多少种不同的方式填补剩下的空位,使得门能够打开?请将答案对 $10^{9}+7$ 取模。
输入格式
第一行输入一个整数 $n$,满足 $2 \leq n \leq 1000000$。
第二行输入 $n$ 个整数 $p_{1},p_{2},...,p_{n}$,其中 $0 \leq p_{i} \leq n$。如果 $p_{i}=0$ 表示该位置有空,需要填补;如果 $p_{i} \geq 1$,表示该位置的值已经确定。
保证如果 $i \neq j$ 且 $p_{i},p_{j} \geq 1$,则 $p_{i} \neq p_{j}$。
输出格式
输出能够填补空位并打开门的方案数,对 $1000000007$ 取模。
说明/提示
在第一个样例中,4 个元素都未被固定。共有 4 个满足条件的排列:(1,2,3,4)、(1,4,3,2)、(3,2,1,4)、(3,4,1,2)。
在第二个样例中,$p_{3}=1$ 且 $p_{4}=2$ 已被固定。满足条件的排列有两种:(3,4,1,2,5)、(5,4,1,2,3)。
由 ChatGPT 5 翻译