CF708C Centroids

Tree is a connected acyclic graph. Suppose you are given a tree consisting of $ n $ vertices. The vertex of this tree is called centroid if the size of each connected component that appears if this vertex is removed from the tree doesn't exceed 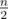. You are given a tree of size $ n $ and can perform no more than one edge replacement. Edge replacement is the operation of removing one edge from the tree (without deleting incident vertices) and inserting one new edge (without adding new vertices) in such a way that the graph remains a tree. For each vertex you have to determine if it's possible to make it centroid by performing no more than one edge replacement.

N/A

N/A

In the first sample each vertex can be made a centroid. For example, in order to turn vertex $ 1 $ to centroid one have to replace the edge $ (2,3) $ with the edge $ (1,3) $ .