Nuclear Fusion

## 题目描述 一道化学题。 你有n个原子，每个原子都有它的“原子序数”（即排在元素周期表中的第几个）。 你可以将任意两个原子合成为一个新的原子（新原子原子序数=两个融合的原子的原子序数之和）。新的原子也可以继续合成。 这个问题的困难在于，它只能将两个原子合成一个新原子，而不允许将一个原子分裂成几个原子。 你的任务是：将已有的n个原子合成为k个希望得到的新原子 新原子将给出 ## 输入格式 第一行：整数n和k( 1<=k<=n<=17) 第二行：n个已有的原子的符号（以空格分隔） 原子的符号与化学元素周期表中的符号一致，可能有相同的多个原子 第三行：k个希望得到的新原子的符号（以空格分隔） ## 输出格式 如果不可能合成所需的原子，请在的情况下打印“NO”（没有引号） 否则，第一行输出“YES” 第2-k+1行，以x1+x2+x3……-&gt;yi格式输出，xi是已有的原子，yi是希望得到的原子（详情可参考示例） ## 说明 原子序数和元素周期表请自行百度（原子序数<=100） 注意：原子的合成不是化学方程式，而只是原子序数相加 第一个例子的反应如下： 

There is the following puzzle popular among nuclear physicists. A reactor contains a set of $ n $ atoms of some chemical elements. We shall understand the phrase "atomic number" as the number of this atom's element in the periodic table of the chemical elements. You are allowed to take any two different atoms and fuse a new one from them. That results in a new atom, whose number is equal to the sum of the numbers of original atoms. The fusion operation can be performed several times. The aim is getting a new pregiven set of $ k $ atoms. The puzzle's difficulty is that it is only allowed to fuse two atoms into one, it is not allowed to split an atom into several atoms. You are suggested to try to solve the puzzle.

The first line contains two integers $ n $ and $ k $ ( $ 1<=k<=n<=17 $ ). The second line contains space-separated symbols of elements of $ n $ atoms, which are available from the start. The third line contains space-separated symbols of elements of $ k $ atoms which need to be the result of the fusion. The symbols of the elements coincide with the symbols from the periodic table of the chemical elements. The atomic numbers do not exceed $ 100 $ (elements possessing larger numbers are highly unstable). Some atoms can have identical numbers (that is, there can be several atoms of the same element). The sum of numbers of initial atoms is equal to the sum of numbers of the atoms that need to be synthesized.

If it is impossible to synthesize the required atoms, print "NO" without the quotes. Otherwise, print on the first line «YES», and on the next $ k $ lines print the way of synthesizing each of $ k $ atoms as equations. Each equation has the following form: " $ x_{1} $ + $ x_{2} $ + $ ... $ + $ x_{t} $ -> $ y_{i} $ ", where $ x_{j} $ is the symbol of the element of some atom from the original set, and $ y_{i} $ is the symbol of the element of some atom from the resulting set. Each atom from the input data should occur in the output data exactly one time. The order of summands in the equations, as well as the output order does not matter. If there are several solutions, print any of them. For a better understanding of the output format, see the samples.

10 3
Mn Co Li Mg C P F Zn Sc K
Sn Pt Y

YES
Mn+C+K->Sn
Co+Zn+Sc->Pt
Li+Mg+P+F->Y

2 1
H H
He

YES
H+H->He

2 2
Bk Fm
Cf Es

NO

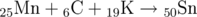
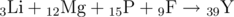
The reactions from the first example possess the following form (the atomic number is written below and to the left of the element):    To find a periodic table of the chemical elements, you may use your favorite search engine. The pretest set contains each of the first $ 100 $ elements of the periodic table at least once. You can use that information to check for misprints.