CF734E Anton and Tree
题目描述
Anton 在他的花园里种了一棵树。如果你忘了的话,树是一种连通且无环的无向图。
这棵树有 $n$ 个顶点,每个顶点被涂成黑色或白色。Anton 不喜欢多种颜色的树,所以他想将整棵树变成同一种颜色(全黑或全白)。
为了改变颜色,Anton 只能使用一种操作。我们用 $paint(v)$ 表示这个操作,其中 $v$ 是树上的某个顶点。这个操作会改变所有顶点 $u$ 的颜色,满足从 $v$ 到 $u$ 的最短路径上的所有顶点(包括 $v$ 和 $u$)颜色都相同。例如,下图中:
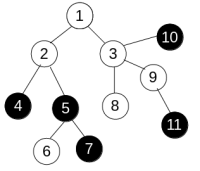
对顶点 $3$ 执行 $paint(3)$ 操作后,变为如下:

Anton 想知道最少需要执行多少次操作,才能使所有顶点的颜色都一致。
输入格式
输入的第一行是一个整数 $n$($1 \leq n \leq 200000$),表示树中顶点的数量。
第二行包含 $n$ 个整数 $color_{i}$($0 \leq color_{i} \leq 1$),表示每个顶点的颜色。$color_{i}=0$ 表示第 $i$ 个顶点初始为白色,$color_{i}=1$ 表示初始为黑色。
接下来有 $n-1$ 行,每行包含两个整数 $u_{i}$ 和 $v_{i}$($1 \leq u_{i},v_{i} \leq n,u_{i} \neq v_{i}$),表示有一条边连接顶点 $u_{i}$ 和 $v_{i}$。保证所有的 $(u_i, v_i)$ 都不同,即没有重边。
输出格式
输出一个整数,表示 Anton 至少需要多少次操作才能使整棵树颜色统一为黑色或白色。
说明/提示
对于第一个样例,树结构如图。如果我们先对顶点 $3$ 执行 $paint(3)$ 操作,再对顶点 $6$ 执行一次操作,整棵树就会变成全黑,因此答案为 $2$。
对于第二个样例,整棵树已经是全白,不需要操作,所以答案为 $0$。
由 ChatGPT 5 翻译